Question

【题目】把一副三角板ABC与ABD摆成如图所示的直二面角D﹣AB﹣C，（其中BD=2AD，BC=AC）则异面直线DC，AB所成角的正切值为（ ）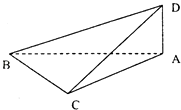

A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：以A为原点，AB、AD所在直线分别为y轴和x轴，建立如图坐标系，
Rt△ABD中，AD：AB：BD=1： ：2，
Rt△ABC中，AC：AB：BC=1： ：1，
设AD= ，则AB= ，BC=AC= ，
则A（0，0，0），B（0，﹣ ，0），C（ ，﹣ ，0），D（0，0， ），
∴ =（0，﹣ ，0）， =（ ，﹣ ，﹣ ），
设异面直线DC，AB所成角为θ，
则cosθ= = = ，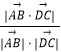
∴sinθ= = ，
∴异面直线DC，AB所成角的正切值tanθ= = ．
故选：D．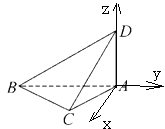

【考点精析】关于本题考查的异面直线及其所成的角，需要了解异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能得出正确答案．