
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:


(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频数分布直方图;
(3)若成绩在75.585.5分的学生为二等奖,问获得二等奖的学生约为多少人?
【答案】(1)答案见解析 (2)答案见解析 (3)234人
【解析】
(1)在频率分布表中,各组的频数![]() 频率
频率![]() 样本容量,再根据频率的和等于1建立等式解之即可;
样本容量,再根据频率的和等于1建立等式解之即可;
(2)根据频率分布表补全频数分布直方图;
(3)成绩在![]() 分的学生占成绩在
分的学生占成绩在![]() 分的学生的
分的学生的![]() ,进而估算出频率,结合共有900名学生参加了这次竞赛可得答案.;
,进而估算出频率,结合共有900名学生参加了这次竞赛可得答案.;
解:(1)由已知样本容量为50,故第二组的频数为![]() ,
,
第三组的频率为![]() ,
,
第四组的频数为:![]() ,频率为:
,频率为:![]() ,
,
故频率分布表为:
分组 | 频数 | 频率 |
| 4 | 0.08 |
| 8 | 0.16 |
| 10 | 0.20 |
| 16 | 0.32 |
| 12 | 0.24 |
合计 | 50 | 1.00 |
(2)如图:
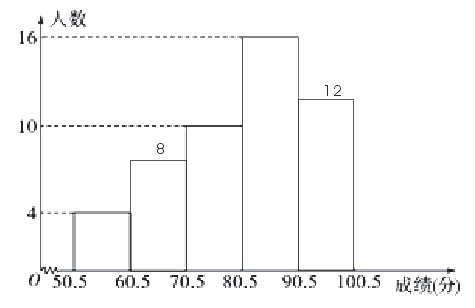
(3)成绩在75.580.5分的学生占70.580.5分的学生的![]() ,因为成绩在70.580.5分的学生频率为0.2 ,所以成绩在75.580.5分的学生频率为0.1 ,
,因为成绩在70.580.5分的学生频率为0.2 ,所以成绩在75.580.5分的学生频率为0.1 ,
成绩在80.585.5分的学生占80.590.5分的学生的![]() ,因为成绩在80.590.5分的学生频率为0.32 ,所以成绩在80.585.5分的学生频率为0.16
,因为成绩在80.590.5分的学生频率为0.32 ,所以成绩在80.585.5分的学生频率为0.16
所以成绩在75.585.5分的学生频率为0.26,由于有900名学生参加了这次竞赛,
所以该校获得二等奖的学生约为0.26900=234(人)


科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,且质量指标值大于或等于![]() 的产品为优质产品.现用两种新配方(分别称为
的产品为优质产品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了
配方)做试验,各生产了![]() 件这种产品,并测量了每件产品的质量指标值(都在区间
件这种产品,并测量了每件产品的质量指标值(都在区间![]() 内),将这些数据分成
内),将这些数据分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:

已知这![]() 种配方生产的产品利润
种配方生产的产品利润![]() (单位:百元)与其质量指标值
(单位:百元)与其质量指标值![]() 的关系式均为
的关系式均为 .
.
若以上面数据的频率作为概率,分别从用![]() 配方和
配方和![]() 配方生产的产品中随机抽取一件,且抽取的这
配方生产的产品中随机抽取一件,且抽取的这![]() 件产品相互独立,则抽得的这两件产品利润之和为
件产品相互独立,则抽得的这两件产品利润之和为![]() 的概率为( )
的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .过抛物线
.过抛物线![]() 上一点
上一点![]() 作
作![]() 的切线
的切线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.
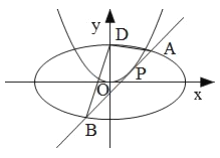
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在直线![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com