
【题目】已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=100.
(1)求数列{bn}的通项bn;
(2)设数列{an}的通项an=loga(1+ ![]() ),a>0,且a≠1,记Sn是数列{an}的前n项的和.试比较Sn与
),a>0,且a≠1,记Sn是数列{an}的前n项的和.试比较Sn与 ![]() logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
【答案】
(1)解:设数列{bn}的公差为d,由题意得:b1=1,
10b1+ ![]() =100.
=100.
解得 ![]() ,
,
∴bn=1+2(n1﹣)=2n﹣1.
(2)解:an=loga(1+ ![]() )=
)= ![]() =
= ![]() ,a>0,且a≠1,
,a>0,且a≠1,
Sn=loga(1+1)+ ![]() +…+
+…+ ![]()
= ![]() .
.
![]() logabn+1=
logabn+1= ![]() =
= ![]() .
.
可先比较(1+1)(1+ ![]() )…(1+
)…(1+ ![]() )与
)与 ![]() 的大小.
的大小.
取n=1,有(1+1)> ![]() ;
;
取n=2,有(1+1)(1+ ![]() )>
)> ![]() .
.
由此推测:(1+1)(1+ ![]() )…(1+
)…(1+ ![]() )>
)> ![]() …①
…①
下面用数学归纳法证明①式:
(i)当n=1时,已验证①式成立.
(ii)假设当n=k (k≥1)时,①式成立,即
(1+1)(1+ ![]() )…(1+
)…(1+ ![]() )>
)> ![]() ,
,
那么,当n=k+1时,(1+1)(1+ ![]() )…(1+
)…(1+ ![]() )(1+
)(1+ ![]() )
)
> ![]() (1+
(1+ ![]() )=
)= ![]() (2k+2)
(2k+2)
∵[ ![]() (2k+2)]2﹣[
(2k+2)]2﹣[ ![]() ]2
]2
= ![]() =
= ![]() >0,
>0,
∴ ![]() (2k+2)>
(2k+2)> ![]() =
= ![]()
因而 (1+1)(1+ ![]() )…(1+
)…(1+ ![]() )(1+
)(1+ ![]() )>
)> ![]() .
.
这就是说①式,当n=k+1时也成立.
由(i),(ii)知,①式对任何正整数n都成立.
利用函数y=logax的单调性,得结论:
当a>1时,Sn> ![]() logabn+1;
logabn+1;
当0<a<1时,Sn< ![]() logabn+1.
logabn+1.
或利用 ![]() =
= ![]() >
> ![]() ,证明
,证明 ![]() …
… ![]() >
> ![]() ,即可证明.
,即可证明.
【解析】(1)利用等差数列的通项公式及其前n项和公式即可得出;(2)an=loga(1+ ![]() )=
)= ![]() =
= ![]() ,a>0,且a≠1,Sn=
,a>0,且a≠1,Sn= ![]() .
. ![]() logabn+1=
logabn+1= ![]() .可先比较(1+1)(1+
.可先比较(1+1)(1+ ![]() )…(1+
)…(1+ ![]() )与
)与 ![]() 的大小.猜想:(1+1)(1+
的大小.猜想:(1+1)(1+ ![]() )…(1+
)…(1+ ![]() )>
)> ![]() ,利用数学归纳法证明即可得出.
,利用数学归纳法证明即可得出.
【考点精析】根据题目的已知条件,利用等差数列的通项公式(及其变式)和数列的前n项和的相关知识可以得到问题的答案,需要掌握通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系 .
.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】已知实数x、y满足  ,目标函数z=x+ay.
,目标函数z=x+ay.
(1)当a=﹣2时,求目标函数z的取值范围;
(2)若使目标函数取得最小值的最优解有无数个,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在“普及环保知识节”后,为了进一步增强环保意识,从本校学生中随机抽取了一批学生参加环保基础知识测试.经统计,这批学生测试的分数全部介于75至100之间.将数据分成以下5组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到如图所示的频率分布直方图. 
(Ⅰ)求a的值;
(Ⅱ)现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生座谈,求每组抽取的学生人数;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计随机抽取学生所得测试分数的平均值在第几组(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() 的图象经过点A(1,1),B(2,﹣1).
的图象经过点A(1,1),B(2,﹣1).
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,+∞)上的单调性并用定义证明;
(3)求f(x)在区间[ ![]() ,1]上的值域.
,1]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产三种型号的轿车,产量分别是1600辆、6000辆和2000辆,为检验公司的产品质量,现从这三种型号的轿车种抽取48辆进行检验,这三种型号的轿车依次应抽取 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|0≤x≤2},B={y|1≤y≤2},若对于函数y=f(x),其定义域为A,值域为B,则这个函数的图象可能是( )
A.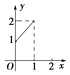
B.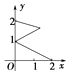
C.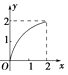
D.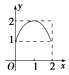
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线E:y2=2px(p>0)的焦点,点A(3,m)在抛物线E上,且|AF|=4. 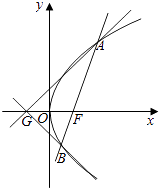
(1)求抛物线E的方程;
(2)已知点G(﹣1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com