【题目】如果函数
在定义域内存在区间
，使得该函数在区间
上的值域为
，则称函数
是该定义域上的“和谐函数”.
（1）求证：函数
是“和谐函数”；
（2）若函数
是“和谐函数”，求实数
的取值范围.
【答案】（1）见解析；（2）
【解析】试题分析：（1）利用“和谐函数”的定义将问题转化为
，再验证进行求解；（2）利用“和谐函数”的定义将问题转化为
和
的图像至少有2个交点，再利用整体换元和数形结合思想进行求解.
试题解析：（1）要证：存在区间
使得
在
上的值域为
，
又由于
是一个单调递増的函数，且定义域为
故只需证存在实数
满足
,且有
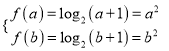
观察得
， 
即存在
符合题意
故函数
是“和谐函数”
（2）由题，即存在实数
满足
，使得
在区间
上的值域为
，
由于
单调递増，从而有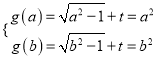
，
该方程组等价于方程
在
有至少2个解，
即
在
上至少有2个解，
即
和
的图像至少有2个交点，
记
，则
，从而有
，
记
，配方得
，
又
，作出
的图像可知， 
时有两个交点，
综上， 
的取值范围为
.
快乐小博士巩固与提高系列答案科目：高中数学 来源： 题型：
【题目】下面有命题：
①y=|sinx-
|的周期是2π；
②y=sinx+sin|x|的值域是[0,2] ；
③方程cosx=lgx有三解;
④
为正实数,
在
上递增，那么的取值范围是
；
⑤在y=3sin(2x+
)中,若f(x
)=f(x2)=0,则x1-x2必为
的整数倍;
⑥若A、B是锐角△ABC的两个内角，则点P（cosB－sinA，sinB－cosA)在第二象限;
⑦在
中,若
,则钝角三角形。
其中真命题个数为( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AB＝5，AA1＝4，点D是AB的中点．
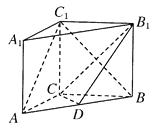
(1)求证：AC⊥BC1；
(2)求证：AC1∥平面CDB1；
(3)求异面直线AC1与B1C所成角的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知F1（﹣c，0）、F2（c，0）分别是椭圆G： 
的左、右焦点，点M是椭圆上一点，且MF2⊥F1F2 ， |MF1|﹣|MF2|= 
a．
（1）求椭圆G的方程；
（2）若斜率为1的直线l与椭圆G交于A、B两点，以AB为底作等腰三角形，顶点为P（﹣3，2），求△PAB的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
是两条不同的直线， 
是三个不同的平面，给出下列四个命题：
①若
，则
②若
，则
③若
，则
④若
，则
其中正确命题的序号是（ ）
A. ①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
科目：高中数学 来源： 题型：
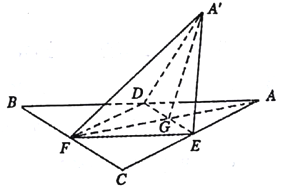
【题目】如图，等边三角形
的中线
与中位线
相交于
，已知
是
绕
旋转过程中的一个图形，给出以下四个命题：①
平面
；②平面
平面
；③动点
在平面
上的射影在线段
上；④异面直线
与
不可能垂直. 其中正确命题的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C对应的边分别是a，b，c，已知cos2A﹣3cos（B+C）=1．
（Ⅰ）求角A的大小；
（Ⅱ）若△ABC的面积S=5 
，b=5，求sinBsinC的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
