
【题目】如图,三棱锥![]() 中,底面
中,底面![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() ,
, ![]() .
.
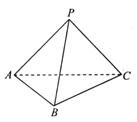
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)通过证明线面垂直,由面面垂直的判定定理,得出面面垂直;(2)先作出二面角![]() 的平面角,再证明,再由余弦定理求出二面角的余弦值。
的平面角,再证明,再由余弦定理求出二面角的余弦值。
试题解析:(1)取AC的中点O,连接BO,PO.
因为ABC是边长为2的正三角形,所以BO⊥AC,BO=![]() .
.
因为PA⊥PC,所以PO=![]() .
.
因为PB=2,所以OP2+OB2==PB2,所以PO⊥OB.
因为AC,OP为相交直线,所以BO⊥平面PAC.
又OB平面ABC,所以平面PAB⊥平面ABC.
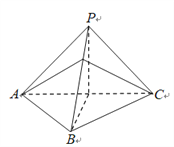
(2)因为PA=PB,BA=BC,所以![]() ≌
≌![]() .
.
过点A作![]() 于D,则
于D,则![]() .
.
所以![]() 为所求二面角A﹣PB﹣C 的平面角.
为所求二面角A﹣PB﹣C 的平面角.
因为PA=PC,PA⊥PC,AC=2,所以![]() .
.
在![]() 中,求得
中,求得![]() ,同理
,同理![]() .
.
在![]() 中,由余弦定理,得
中,由余弦定理,得![]() .
.
所以,二面角A﹣PB﹣C的余弦值为![]() .
.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=asinωx+bcosωx(ω>0)的定义域为R,最小正周期为π,且对任意实数x,恒有![]() 成立.
成立.

(1)求实数a和b的值;
(2)作出函数f(x)在区间(0,π)上的大致图象;
(3)若两相异实数x1、x2∈(0,π),且满足f(x1)=f(x2),求f(x1+x2)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在某海滨城市A附近的海面出现台风活动.据监测,目前台风中心位于城市A的东偏南60°方向、距城市A300km的海面点P处,并以20km/h的速度向西偏北30°方向移动.如果台风影响的范围是以台风中心为圆心的圆形区域,半径为![]() km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.
km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为了保护环境,减少空气污染,某空气净化器制造厂,决定投入生产某种惠民型的空气净化器.根据以往的生产销售经验得到年生产销售的统计规律如下:①年固定生产成本为2万元;②每生产该型号空气净化器1百台,成本增加1万元;③年生产x百台的销售收入 (万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(1)为使该产品的生产不亏本,年产量x应控制在什么范围内?
(2)该产品生产多少台时,可使年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,苹果销量约占20%,三星销量约占30%).根据该图,以下结论中一定正确的是( )
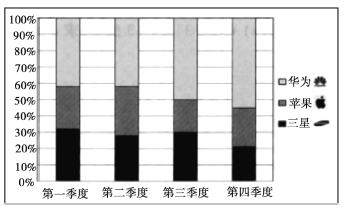
A.华为的全年销量最大B.苹果第二季度的销量大于第三季度的销量
C.华为销量最大的是第四季度D.三星销量最小的是第四季度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:函数![]() 且|f(a)|<2,命题Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
且|f(a)|<2,命题Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
(1)分别求命题P、Q为真命题时的实数a的取值范围;
(2)当实数a取何范围时,命题P、Q中有且仅有一个为真命题;
(3)设P、Q皆为真时a的取值范围为集合S,![]() ,若RTS,求m的取值范围.
,若RTS,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
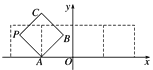
【题目】如图所示,放置的边长为1的正方形![]() 沿
沿![]() 轴滚动,点
轴滚动,点![]() 恰好经过原点.设顶点
恰好经过原点.设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 有下列判断:
有下列判断:
①若![]() ,则函数
,则函数![]() 是偶函数;
是偶函数;
②对任意的![]() ,都有
,都有![]() ;
;
③函数![]() 在区间
在区间![]() 上单调递减;
上单调递减;
④函数![]() 在区间
在区间![]() 上是减函数.
上是减函数.
其中判断正确的序号是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人群中各种血型的人所占的比例见下表:
血腥 | A | B | AB | O |
该血型的人所占的比例/% | 28 | 29 | 8 | 35 |
已知同种血型的人可以互相输血,O型血可以给任一种血型的人输血,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血.该人群中的小明是B型血,若他因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com