
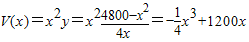 ,求导函数,确定函数的极值,极大值,也是最大值.
,求导函数,确定函数的极值,极大值,也是最大值.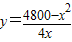 ,0<x<60. (6分)
,0<x<60. (6分)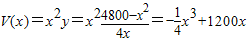 ,(10分)
,(10分)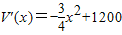 ,令V′(x)=0,得x=40,(12分)
,令V′(x)=0,得x=40,(12分)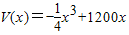 ,在x=40时取得极大值,也是最大值,其值为32000cm3.
,在x=40时取得极大值,也是最大值,其值为32000cm3.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
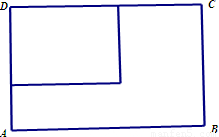
 (2012•江苏一模)现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)
(2012•江苏一模)现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省苏北四市(徐、连、淮、宿)高三元月调研测试数学试卷 题型:解答题
(本小题满分14分)现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失。如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)

(1)求出x 与 y 的关系式;
(2)求该铁皮盒体积V的最大值;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省徐州市高三(上)第一次质量检测数学试卷(解析版) 题型:解答题
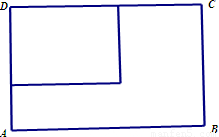
查看答案和解析>>
科目:高中数学 来源:2012年江苏省苏北四市高考数学一模试卷(解析版) 题型:解答题
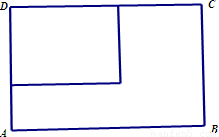
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com