，tanN=-2.建立适当的坐标系，求出以M、N为焦点且过点P的椭圆方程.
思路解析：建立适当的坐标系后,易得PM、PN的方程，则有了P点坐标，待定系数法可求椭圆方程；也可以解△PMN，得三边长后再建系求方程.
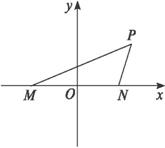
解法一：以MN所在直线为x轴，线段MN的垂直平分线为y轴建立直角坐标系，如图所示.
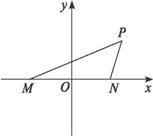
设所求椭圆方程为
+
=1(a＞b＞0).分别记 M、N点的坐标为(-c，0)、(c，0).
由tan∠PMN=
,tan∠PNx=tan(π-∠PNM)=2得直线PM、PN的方程分别是
y=
（x+c），y=2（x-c）.
联立解得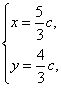
即P(
c，
c).
又S△MNP=
|MN|·y=
·2c·
c=
c2=1.
∴c=
，从而点P为（
，
）.
将点P的坐标代入椭圆方程,得
+
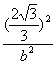=1. ①
由题意,得a2-c2=b2.
∴a2-
=b2.②
由①②联立得方程组
解得a2=
，b2=3.
∴椭圆的标准方程是
+
=1.
解法二：同解法一，得c=
，P(
，
).
∴|PM|=
=
=
.
∴|PN|=（x-c）2+y2
=
=
.
∴a=
（|PM|+|PN|）=
，从而b2=a2-c2=
-
=3.
∴椭圆方程为
+
=1.
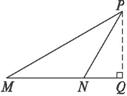
解法三：如图所示，过P作PQ⊥MN，PQ交MN的延长线于Q，
∵∠MNP=π-∠PNQ，
∴tan∠MNP=tan（π-∠PNQ）=-2.
∴tanPNQ=2.
在Rt△PNQ中，tan∠PNQ=
.
∴PQ=2NQ，即NQ=
PQ.
同理,PQ=
MQ，∴MQ=2PQ.∴MN=MQ-NQ=2PQ-
PQ=
PQ.
∵S△MNP=
MN·PQ，∴
·
PQ·PQ=1.
∴PQ=
.∴MQ=2PQ=
，NQ=
.
∴PM=
=
=
，
PN=
=
=
，
MN=
PQ=
·
=
.
以MN所在直线为x轴，MN的中垂线为y轴建立如图所示的坐标系.
设椭圆的标准方程是
+
=1（a＞b＞0）,
则2a=|PM|+|PN|=
+
=
,
2c=|MN|=
.
∴a=
,c=
.
∴b2=a2-c2=(
)2-(
)2=3.
∴椭圆的标准方程是
+
=1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
,tan∠MNP=2,建立适当坐标系，求以M、N为焦点且过点P的双曲线方程.
,tanN=-2，建立适当坐标系,求出以MN为焦点且过P点的椭圆方程. 
,tan∠N=-2，建立适当坐标系,求出以MN为焦点且过P点的椭圆方程.