
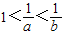 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )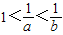 ,则易得0<b<a<1,则可以根据指数的性质:logab>1,0<logba<1,及logab•logba=1,对四个答案逐一进行分析,易得答案
,则易得0<b<a<1,则可以根据指数的性质:logab>1,0<logba<1,及logab•logba=1,对四个答案逐一进行分析,易得答案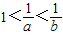 ,
,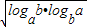 =2,故B正确.
=2,故B正确.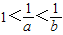 ,
, ,a=
,a=



科目:高中数学 来源: 题型:
 |
| y |
查看答案和解析>>
科目:高中数学 来源:2014届云南省大理州高二月考文科数学卷(解析版) 题型:选择题
设某大学的女生体重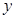 (单位:kg)与身高
(单位:kg)与身高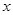 (单位:cm)
具有线性相关关系,根据一组样本数据(
(单位:cm)
具有线性相关关系,根据一组样本数据(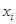 ,
,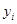 )(i=1,2,…,n),用最小二乘法建立的回归方程为
)(i=1,2,…,n),用最小二乘法建立的回归方程为
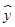 =0.85x-85.71,则下列结论中不正确的是 ( )
=0.85x-85.71,则下列结论中不正确的是 ( )
A.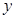 与
与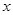 具有正的线性相关关系
具有正的线性相关关系
B.回归直线过样本点的中心(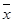 ,
,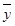 )
)
C.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
D.若该大学某女生身高增加1cm,则其体重约增加0.85kg
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省度高二下学期第二次检测考试理科数学试卷(解析版) 题型:选择题
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为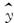 =0.85x-85.71,则下列结论中不正确的是( ).
=0.85x-85.71,则下列结论中不正确的是( ).
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心(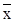 ,
,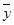 )
)
C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(湖南卷解析版) 题型:选择题
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A、y与x具有正的线性相关关系
B、回归直线过样本点的中心( ,
,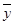 )
)
C、若该大学某女生身高增加1cm,则其体重约增加0.85kg
D、若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试文科数学(湖南卷解析版) 题型:选择题
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A、y与x具有正的线性相关关系
B、回归直线过样本点的中心(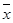 ,
,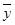 )
)
C、若该大学某女生身高增加1cm,则其体重约增加0.85kg
D、若该大学某女生身高为170cm,则可断定其体重必为58.79kg
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com