
【题目】如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF= ![]() AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( ) 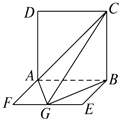
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵ABCD是正方形,∴CB⊥AB, ∵面ABCD⊥面ABEF且交于AB,∴CB⊥面ABEF.
∵AG,GB面ABEF,∴CB⊥AG,CB⊥BG,
又AD=2a,AF=a,ABEF是矩形,G是EF的中点,
∴AG=BG= ![]() a,AB=2a,∴AB2=AG2+BG2 , ∴AG⊥BG,
a,AB=2a,∴AB2=AG2+BG2 , ∴AG⊥BG,
∵BG∩BC=B,∴AG⊥平面CBG,而AG面AGC,故平面AGC⊥平面BGC.
在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC,∴∠BGH是GB与平面AGC所成的角.
在Rt△CBG中,BH= ![]() =
= ![]() ,
,
∵BG= ![]() a,∴sin∠BGH=
a,∴sin∠BGH= ![]() =
= ![]() .
.
故选C.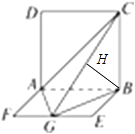
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能正确解答此题.
才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() (a∈R)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
(a∈R)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
(1)若对于任意的x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求实数m的取值范围;
(2)设函数g(x)=(x+1)f(x)﹣b(x﹣1)在[1,e]上有且只有一个零点,求实数b取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,面积为 ![]() 的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.
的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3. 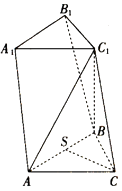
(1)若AB的中点为S,证明:CS⊥C1A.
(2)设 ![]() ,是否存在实数λ,使得直线TB与平面ACC1A1的夹角为
,是否存在实数λ,使得直线TB与平面ACC1A1的夹角为 ![]() ?若存在,求出λ的值;若不存在,请说明理由.
?若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是两条不重合的直线,
是两条不重合的直线, ![]() 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题:
①若 ![]() ,
, ![]() ,则
,则 ![]() ;②若
;②若 ![]() ,
, ![]() ,则
,则 ![]() ;
;
③若 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() ;④若
;④若 ![]() 是异面直线,
是异面直线, ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() .
.
其中真命题是( )
A.①和④
B.①和③
C.③和④
D.①和②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点. (Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求证:OE∥平面PDC;
(Ⅲ)求面PAD与面PBC所成角的大小.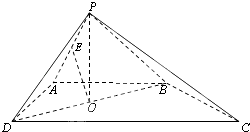
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣3|+ax﹣6(a是常数,a∈R). (Ⅰ)当a=1时,求不等式f(x)≥0的解集;
(Ⅱ)当x∈[﹣1,1]时,不等式f(x)<0恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com