
【题目】从集市上买回来的蔬菜仍存有残留农药,食用时需要清洗数次,统计表中的![]() 表示清洗的次数,
表示清洗的次数,![]() 表示清洗
表示清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量(单位:微克).
千克该蔬菜残留的农药量(单位:微克).
|
|
|
|
|
|
|
|
|
|
|
|
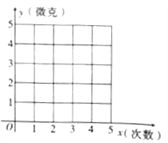
(1)在如图的坐标系中,描出散点图,并根据散点图判断,![]()
![]() 哪一个适宜作为清洗
哪一个适宜作为清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)
千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)
(2)根据判断及下面表格中的数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
表中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)对所求的回归方程进行残差分析.
附:①线性回归方程![]() 中系数计算公式分别为
中系数计算公式分别为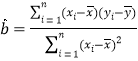 ,
,![]() ;
;
② ,
,![]() 说明模拟效果非常好;
说明模拟效果非常好;
③![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【答案】(1)散点图见解析,用![]() 作为清洗
作为清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量的回归方程类型
千克该蔬菜残留的农药量的回归方程类型
(2) ![]() (3)回归模拟的拟合效果非常好
(3)回归模拟的拟合效果非常好
【解析】分析:(1)将表格中的点描上去,即可判断出来散点图类似指数型增长;
(2)按照给出的公式进行计算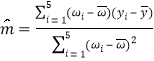 和
和![]() 即可;
即可;
(3)列出表格算出相应的值与给出的值进行比较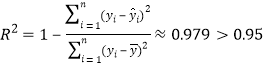 说明模拟效果非常好。
说明模拟效果非常好。
详解:(1)散点图如图,
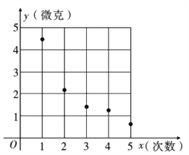
用![]() 作为清洗
作为清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量的回归方程类型.
千克该蔬菜残留的农药量的回归方程类型.
(2)由题知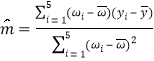
![]() ,
,
![]() ,
,
故所求的回归方程为![]() .
.
(3)列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
所以![]() ,
,![]() ,
,![]() ,
,
所以回归模拟的拟合效果非常好.
点晴:变量间的相关性也是每年高考的必考题,大家在拿到这类题目的时候需按照公式的需求进行运算,运算量相对较大,关注计算是重点。


科目:高中数学 来源: 题型:
【题目】某粮食店经销小麦,年销售量为6000千克,每千克小麦进货价为2.8元,销售价为3.4元,全年进货若干次,每次的进货量均为![]() 千克(
千克(![]() ),运费为100元/次,并且全年小麦的总存储费用为
),运费为100元/次,并且全年小麦的总存储费用为![]() 元.
元.
(1)用![]() (千克)表示该粮食店经销小麦的年利润
(千克)表示该粮食店经销小麦的年利润![]() (元);
(元);
(2)每次进货量为多少千克时,能使年利润![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 分别是
分别是![]() 的中点将
的中点将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 重合于点
重合于点![]() .则下列结论正确的是( )
.则下列结论正确的是( )

A. ![]()
B. 平面![]()
C. 二面角![]() 的余弦值为
的余弦值为![]()
D. 点![]() 在平面
在平面![]() 上的投影是
上的投影是![]() 的外心
的外心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数![]() 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的对称轴方程;
的对称轴方程;
(3)当![]() 时,方程
时,方程![]() 有两个不同的实根,求m的取值范围。
有两个不同的实根,求m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答下列各题:
(1)已知扇形的周长为10cm,面积为4cm2,求扇形圆心角的弧度数.
(2)已知一扇形的圆心角是72°,半径等于20cm,求扇形的面积.
(3)已知一扇形的周长为40cm,求它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初始溶液含杂质2%,每过滤一次可使杂质含量减少![]() .
.
(1)写出杂质含量y与过滤次数n的函数关系式;
(2)过滤7次后的杂质含量是多少?过滤8次后的杂质含量是多少?至少应过滤几次才能使产品达到市场要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为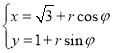 (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
,![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com