
【题目】已知函数![]() .
.
(Ⅰ)(ⅰ)求证:![]() ;
;
(ⅱ)设![]() ,当
,当![]() 时,求实数
时,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,过原点分别作曲线
时,过原点分别作曲线![]() 与
与![]() 的切线
的切线![]() ,已知两切线的斜率互为倒数,证明:
,已知两切线的斜率互为倒数,证明:![]() .
.
【答案】(Ⅰ)(ⅰ)详见解析;(ⅱ)![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
(Ⅰ)(ⅰ)构造函数![]() ,通过求导分析单调性,利用最值即可证明;
,通过求导分析单调性,利用最值即可证明;
(ⅱ)由![]() ,当
,当![]() 时,利用
时,利用![]() 可得函数单调性从而知成立,当
可得函数单调性从而知成立,当![]() 时求导分析单调性找到反例知不成立,从而得解;
时求导分析单调性找到反例知不成立,从而得解;
(Ⅱ)设切线![]() 的方程为
的方程为![]() ,切点为
,切点为![]() ,则
,则![]() ,
,![]() ,可得
,可得![]() 的的方程为
的的方程为![]() ,设
,设![]() 与曲线
与曲线![]() 的切点为
的切点为![]() ,通过求导列方程可得
,通过求导列方程可得![]() ,令
,令![]() ,求导利用单调性即可证得.
,求导利用单调性即可证得.
(Ⅰ)(ⅰ)证明:令![]() ,
,
则![]() ,
,
所以![]() 时,
时,![]() ,
,![]() 时
时![]() ,
,
所以![]() ,即
,即![]() .
.
(ⅱ)![]() ,
,
![]() .
.
a.当![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() ,
,
所以![]() ,
,
所以![]() 在[
在[![]() 上递增,
上递增,
则![]() 恒成立,符合题意.
恒成立,符合题意.
b.当![]() 时,令
时,令![]() ,则
,则
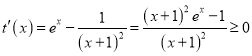 ,所以
,所以![]() 在
在![]() 上递增,且
上递增,且![]() ,则存在
,则存在![]() ,使得
,使得![]() .
.
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
又![]() ,所以
,所以![]() 不恒成立,不合题意.
不恒成立,不合题意.
综合a,b可知,所求实数a的取值范围是![]() .
.
(Ⅱ)证明:设切线![]() 的方程为
的方程为![]() ,切点为
,切点为![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,![]() , 则
, 则![]() .
.
由题意知,切线![]() 的斜率为
的斜率为![]() ,
,![]() 的的方程为
的的方程为![]() .
.
设![]() 与曲线
与曲线![]() 的切点为
的切点为![]() ,
,
则![]() ,
,
所以![]() ,
,![]() .
.
又因为![]() ,
,
消去![]() 和a后 ,整理得
和a后 ,整理得![]() .
.
令![]() ,
,
则![]() ,
,
易知![]() 在
在![]() 上单调递减, 在
上单调递减, 在![]() 上单调递增 .
上单调递增 .
若![]() ,因为
,因为
![]() ,
,![]() ,所以
,所以![]() ,
,
而![]() ,在
,在![]() 上单调递减,
上单调递减,
所以![]() .
.
若![]() ,因为
,因为![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,则
,则![]() ,所以
,所以![]() (舍去).
(舍去).
综上所述:![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】已知集合![]() ,集合
,集合![]() 是集合S的一个含有8个元素的子集.
是集合S的一个含有8个元素的子集.
(1)当![]() 时,设
时,设![]() ,
,
①写出方程![]() 的解(
的解(![]() );
);
②若方程![]() 至少有三组不同的解,写出k的所有可能取值;
至少有三组不同的解,写出k的所有可能取值;
(2)证明:对任意一个X,存在正整数k,使得方程![]()
![]() 至少有三组不同的解.
至少有三组不同的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).![]() 是曲线
是曲线![]() 上的动点,将线段
上的动点,将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到线段
得到线段![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(I)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(II)在(I)的条件下,若射线![]() 与曲线
与曲线![]() ,
,![]() 分别交于
分别交于![]() 两点(除极点外),且有定点
两点(除极点外),且有定点![]() ,求
,求![]() 面积.
面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年时红军长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神.首先在甲、乙、丙、丁四个不同的公园进行支持签名活动.
公园 | 甲 | 乙 | 丙 | 丁 |
获得签名人数 | 45 | 60 | 30 | 15 |
然后在各公园签名的人中按分层抽样的方式抽取10名幸运之星回答问题,从10个关于长征的问题中随机抽取4个问题让幸运之星回答,全部答对的幸运之星获得一份纪念品.
(Ⅰ)求此活动中各公园幸运之星的人数;
(Ⅱ)若乙公园中每位幸运之星对每个问题答对的概率均为![]() ,求恰好2位幸运之星获得纪念品的概率;
,求恰好2位幸运之星获得纪念品的概率;
(Ⅲ)若幸运之星小李对其中8个问题能答对,而另外2个问题答不对,记小李答对的问题数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com