
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)求证:曲线![]() 与
与![]() 在
在![]() 处的切线重合;
处的切线重合;
(Ⅱ)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见证明(Ⅱ)![]()
【解析】
(Ⅰ)分别对两函数求导,求出两函数在![]() 处切线的斜率,再利用点斜式求出切线的直线方程,就可以证明曲线
处切线的斜率,再利用点斜式求出切线的直线方程,就可以证明曲线![]() 与
与![]() 在
在![]() 处的切线重合;
处的切线重合;
(Ⅱ)方法1:构造![]() 对
对![]() 求导得到
求导得到![]() ,对
,对![]() 进行分类讨论,利用函数的单调性,综合分析,最后求出实数
进行分类讨论,利用函数的单调性,综合分析,最后求出实数![]() 的取值范围。
的取值范围。
方法2:![]() 可得
可得![]() (
(![]() ),构造新函数
),构造新函数
设![]() ,求导,对
,求导,对![]() 进行分类讨论,利用函数的单调性,综合分析,最后求出实数
进行分类讨论,利用函数的单调性,综合分析,最后求出实数![]() 的取值范围。
的取值范围。
证明:(Ⅰ)![]()
![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
![]()
![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
所以切线重合.
(Ⅱ)(方法1):令![]()
![]()
①当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时取“
时取“![]() ”,
”,
![]() 在
在![]() 递减,
递减,![]() ,
,![]() 不恒成立.
不恒成立.
②当![]() 时,
时,![]() ,
,
(i)当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 递减,
递减,
![]() ,
,![]() 在
在![]() 递减,
递减,
![]() ,
,![]() 不恒成立.
不恒成立.
(ii)当![]() 时,
时,![]() ,
,![]() 在
在![]() 递增,
递增,
![]() ,
,![]() 在
在![]() 递增,
递增,
![]() ,
,![]() 恒成立.
恒成立.
综上,![]() .
.
(Ⅱ)(方法2):
![]() ,
,
![]() (
(![]() ),
),
设![]() ,
,
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() 在
在![]() 递减,
递减,![]()
![]() ,与已知矛盾
,与已知矛盾
![]() ,
,![]()
①![]() ,
,![]() ,
,![]()
![]() 在
在![]() 递增
递增![]() ,满足题意
,满足题意
②当![]() 时,
时,![]()
![]() ,
,![]() ,
,![]() 在
在![]() 递减,
递减,![]() ,
,
不满足题意
综上,![]()


科目:高中数学 来源: 题型:
【题目】已知圆C过定点![]() ,且与直线
,且与直线![]() 相切,圆心C的轨迹为E,曲线E与直线l:
相切,圆心C的轨迹为E,曲线E与直线l:![]() (
(![]() )相交于A,B两点.
)相交于A,B两点.
(1)求曲线E的方程;
(2)当![]() 的面积等于
的面积等于![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆C过定点F(2,0),且与直线x=-2相切,圆心C的轨迹为E,
(1)求圆心C的轨迹E的方程;
(2)若直线l交E与P,Q两点,且线段PQ的中心点坐标(1,1),求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某市高三学生的身体情况,某健康研究协会对该市高三学生组织了两次体测,其中第一次体测的成绩(满分:100分)的频率分布直方图如下图所示,第二次体测的成绩![]() .
.
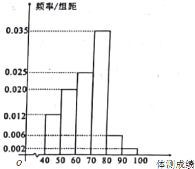
(Ⅰ)试通过计算比较两次体测成绩平均分的高低;
(Ⅱ)若该市有高三学生20000人,记体测成绩在70分以上的同学的身体素质为优秀,假设这20000人都参与了第二次体测,试估计第二次体测中身体素质为优秀的人数;
(Ⅲ)以频率估计概率,若在参与第一次体测的学生中随机抽取4人,记这4人成绩在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个圆锥内作一个内接等边圆柱(一个底面在圆锥的底面上,且轴截面是正方形的圆柱),再在等边圆柱的上底面截得的小圆锥内做一个内接等边圆柱,这样无限的做下去.
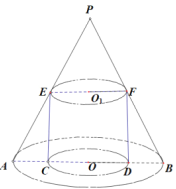
(1)证明这些等边圆柱的体积从大到小排成一个等比数列;
(2)已知这些等边圆柱的体积之和为原来圆锥体积的![]() ,求最大的等边圆柱的体积与圆锥的体积之比.
,求最大的等边圆柱的体积与圆锥的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确是( )

A.A,M,O三点共线B.A,M,O,A1不共面
C.A,M,C,O不共面D.B,B1,O,M共面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,且与坐标轴形成的三角形面积为
,且与坐标轴形成的三角形面积为![]() .求:
.求:
(1)求证:不论![]() 为何实数,直线
为何实数,直线![]() 过定点P;
过定点P;
(2)分别求![]() 和
和![]() 时,所对应的直线条数;
时,所对应的直线条数;
(3)针对![]() 的不同取值,讨论集合
的不同取值,讨论集合![]() 直线
直线![]() 经过P,且与坐标轴围成的三角形面积为
经过P,且与坐标轴围成的三角形面积为![]() 中的元素个数.
中的元素个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com