
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() ,
,![]() 为左焦点,椭圆的离心率为
为左焦点,椭圆的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于点
于点![]() 为
为![]() 上一动点,且在
上一动点,且在![]() 之间移动.
之间移动.
(1)当![]() 取最小值时,求
取最小值时,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的边长恰好是三个连接的自然数,求
的边长恰好是三个连接的自然数,求![]() 面积的最大值.
面积的最大值.

【答案】(1)![]() ,
,![]() .(2)
.(2)![]() .
.
【解析】分析:(1)用![]() 表示出
表示出![]() ,根据基本不等式得出
,根据基本不等式得出![]() 的值,从而得出
的值,从而得出![]() 的方程;
的方程;
(2)用![]() 表示出椭圆的方程,联立方程组得出P点坐标,计算出
表示出椭圆的方程,联立方程组得出P点坐标,计算出![]() 的三边关于
的三边关于![]() 的式子,从而确定
的式子,从而确定![]() 的值,求出
的值,求出![]() 的距离和M到直线PQ的距离,利用二次函数性质得出三角形面积的最大值.
的距离和M到直线PQ的距离,利用二次函数性质得出三角形面积的最大值.
详解:(1)因为![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
所以![]() 取最小值时
取最小值时![]() ,
,
此时抛物线![]() ,此时
,此时![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
设椭圆的标准方程为![]() ,
,![]() ,
,![]() ,
,
由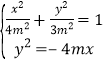 ,得
,得![]() ,
,
所以![]() 或
或![]() (舍去),
(舍去),
代入抛物线方程得![]() ,
,
即![]() ,
,
于是![]() ,
,![]() ,
,![]()
又![]() 的边长恰好是三个连续的自然数,
的边长恰好是三个连续的自然数,
所以![]() ,此时抛物线方程为
,此时抛物线方程为![]() ,
,![]()
则直线![]() 的方程为
的方程为![]() ,
,
联立![]() ,得
,得![]() 或
或![]() (舍去)
(舍去)
于是![]() .
.
所以![]() ,
,
设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
则![]()
当![]() 时,
时,![]() ,
,
所以![]() 的面积最大值为
的面积最大值为![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 .直线
.直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 、
、![]() 、
、![]() 成等比数列,求实数
成等比数列,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某机械厂欲从![]() 米,
米,![]() 米的矩形铁皮中裁剪出一个四边形
米的矩形铁皮中裁剪出一个四边形![]() 加工成某仪器的零件,裁剪要求如下:点
加工成某仪器的零件,裁剪要求如下:点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
,![]() .设
.设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (单位:平方米).
(单位:平方米).

(1)求![]() 关于
关于![]() 的函数关系式,求出定义域;
的函数关系式,求出定义域;
(2)当![]() 的长为何值时,裁剪出的四边形
的长为何值时,裁剪出的四边形![]() 的面积最小,并求出最小值.
的面积最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解重庆市高中学生在面对新高考模式“3+1+2”的科目选择中,物理与历史的二选一是否与性别有关,某高中随机对该校50名高一学生进行了问卷调查得到相关数据如下列联表:
选物理 | 选历史 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
己知在这50人中随机抽取1人,抽到选物理的人的概率为![]() 。
。
(1)请将上面的列联表补充完整,并判断是否有99.5%的把握认为物理与历史的二选一与性别有关?
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式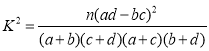 ,其中
,其中![]() 为样本容量)
为样本容量)
(2)己知在选物理的10位女生中有3人选择了化学、地理,有5人选择了化学、生物,有2人选择了生物、地理,现从这10人中抽取3人进行更详细的学科意愿调查,记抽到的3人中选择化学的有X人,求随机变量X的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,
时,![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
![]() Ⅱ
Ⅱ![]() 设
设![]() 是定义在
是定义在![]() 上的函数,在
上的函数,在![]() 内任取
内任取![]() 个数
个数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() ,令
,令![]() ,
,![]() ,如果存在一个常数
,如果存在一个常数![]() ,使得
,使得![]() 恒成立,则称函数
恒成立,则称函数![]() 在区间
在区间![]() 上的具有性质P.试判断函数
上的具有性质P.试判断函数![]() 在区间
在区间![]() 上是否具有性质P?若具有性质P,请求出M的最小值;若不具有性质P,请说明理由.
上是否具有性质P?若具有性质P,请求出M的最小值;若不具有性质P,请说明理由.![]() 注:
注:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 是定义域为R的奇函数,其中m是常数.
是定义域为R的奇函数,其中m是常数.
(Ⅰ)判断f(x)的单调性,并用定义证明;
(Ⅱ)若对任意x∈[﹣3,1],有f(tx)+f(2t﹣1)≤0恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某池塘中原有一块浮草,浮草蔓延后的面积![]() (平方米)与时间
(平方米)与时间![]() (月)之间的函数关系式是
(月)之间的函数关系式是![]() 且
且![]() ,它的图象如图所示,给出以下命题:①池塘中原有浮草的面积是
,它的图象如图所示,给出以下命题:①池塘中原有浮草的面积是![]() 平方米;②第
平方米;②第![]() 个月浮草的面积超过
个月浮草的面积超过![]() 平方米;③浮草每月增加的面积都相等;④若浮草面积达到
平方米;③浮草每月增加的面积都相等;④若浮草面积达到![]() 平方米,
平方米,![]() 平方米,
平方米,![]() 平方米所经过的时间分别为
平方米所经过的时间分别为![]() ,则
,则![]() .其中正确命题的序号有_____.(注:请写出所有正确结论的序号)
.其中正确命题的序号有_____.(注:请写出所有正确结论的序号)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学届的震动。在1859年的时候,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想。在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,
的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 768 B. 144 C. 767 D. 145
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com