
在△ 中,
中,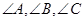 的对边分别为
的对边分别为 ,若
,若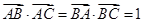 .
.
(1)求证: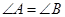 ;
;
(2)求边长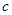 的值;
的值;
(3)若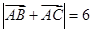 ,求△
,求△ 的面积.
的面积.
(1)详见解析;(2)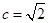 ;(3)
;(3)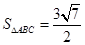 .
.
解析试题分析:(1)将条件中等式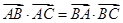 ,通过向量语言转化为角的等式,进而达到证明的目的;(2)结合条件自觉地选择余弦定理的恰当的表达形式,增加条件,从而解出边长
,通过向量语言转化为角的等式,进而达到证明的目的;(2)结合条件自觉地选择余弦定理的恰当的表达形式,增加条件,从而解出边长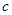 的值;(3)将向量等式
的值;(3)将向量等式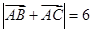 转化为边与角的等式,再结合(1)(2)可解出三边,进而可求出三角形的面积.在解三角形的问题中,关键是结合题目的自身特点,选择正、余弦定理的恰当形式,同时注意边角互化思想的使用.
转化为边与角的等式,再结合(1)(2)可解出三边,进而可求出三角形的面积.在解三角形的问题中,关键是结合题目的自身特点,选择正、余弦定理的恰当形式,同时注意边角互化思想的使用.
试题解析:(1)因为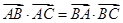 ,所以
,所以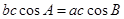 ,即
,即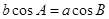 ,
,
由正弦定理得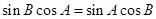 ,所以
,所以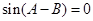 ,
,
因为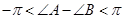 ,所以
,所以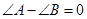 ,所以
,所以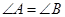 . 4分
. 4分
(2)由(1)知: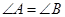 ,所以
,所以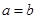 ,再由余弦定理得:
,再由余弦定理得: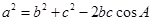 结合条件
结合条件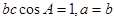 得:
得: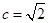 . 8分
. 8分
(3)由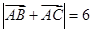 平方得:
平方得: ,又
,又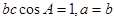 ,
,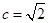 ,得
,得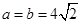 ,从而有
,从而有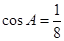 ,则
,则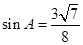 ,所以△
,所以△ 的面积为
的面积为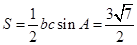 . 12分
. 12分
考点:向量数量积与解三角形综合.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com