
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点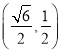 ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】试题分析:(1) 设椭圆![]() 的方程为:
的方程为: ![]()
![]() ,根据已知点和离心率列方程解出a,b,求出椭圆的方程;(2) 由已知直线
,根据已知点和离心率列方程解出a,b,求出椭圆的方程;(2) 由已知直线![]() 过左焦点
过左焦点![]() , 当直线
, 当直线![]() 与
与![]() 轴垂直时,经检验不合题意; 当直线
轴垂直时,经检验不合题意; 当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为:
的方程为: ![]() ,与椭圆方程联立,消去y,得出关于x的一元二次方程,写出韦达定理,根据面积公式求出k的值,可得直线方程.
,与椭圆方程联立,消去y,得出关于x的一元二次方程,写出韦达定理,根据面积公式求出k的值,可得直线方程.
试题解析:
(1)设椭圆![]() 的方程为:
的方程为: ![]()
![]() ,
,
由已知: 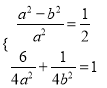 得:
得: ![]() ,
, ![]() ,
,
所以,椭圆![]() 的方程为:
的方程为: ![]() .
.
(2)由已知直线![]() 过左焦点
过左焦点![]() .
.
①当直线![]() 与
与![]() 轴垂直时,
轴垂直时, 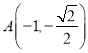 ,
, 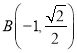 ,此时
,此时![]() ,
,
则![]() ,不满足条件.
,不满足条件.
②当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为:
的方程为: ![]()
由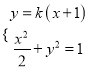 得
得![]()
所以![]() ,
, ![]() ,
,
而![]() ,
,
由已知![]() 得
得![]() ,
,
所以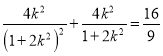 ,则
,则![]() ,所以
,所以![]() ,
,
所以直线![]() 的方程为:
的方程为: ![]() 或
或![]() .
.
点睛: 本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列各组函数f(x)与g(x)的图象相同的是( )
A.f(x)=x,g(x)=( ![]() )2
)2
B.f(x)=x2 , g(x)=(x+1)2
C.f(x)=1,g(x)=x0
D.f(x)=|x|,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了![]() 名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:
名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:
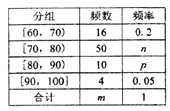

(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值;
的值;
(2)如果用分层抽样的方法,从样本成绩在![]() 和
和![]() 的学生中共抽取
的学生中共抽取![]() 人,再从
人,再从![]() 人中选
人中选![]() 人,
人,
求这![]() 人成绩在
人成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解消费者购物情况,某购物中心在电脑小票中随机抽取![]() 张进行统计,将结果分成6组,分别是:
张进行统计,将结果分成6组,分别是: ![]() ,
, ![]() ,制成如下所示的频率分布直方图(假设消费金额均在
,制成如下所示的频率分布直方图(假设消费金额均在![]() 元的区间内).
元的区间内).
(1)若在消费金额为![]() 元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票来自
元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票来自![]() 元和
元和![]() 元区间(两区间都有)的概率;
元区间(两区间都有)的概率;
(2)为做好春节期间的商场促销活动,商场设计了两种不同的促销方案.

方案一:全场商品打八五折.
方案二:全场购物满100元减20元,满300元减80元,满500元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析:哪种方案优惠力度更大,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连掷一枚均匀的骰子两次,所得向上的点数分别为![]() ,记
,记![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 事件“![]() ”的概率为
”的概率为![]() B. 事件“
B. 事件“![]() 是奇数”与“
是奇数”与“![]() ”互为对立事件
”互为对立事件
C. 事件“![]() ”与“
”与“![]() ”互为互斥事件 D. 事件“
”互为互斥事件 D. 事件“![]() ”的概率为
”的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时, ![]() 平均增加
平均增加![]() 个单位;
个单位;
③老师在某班学号为1~50的50名学生中依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查,这种抽样方法是系统抽样;
其中正确的个数是( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 0
D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是P(万元)和Q(万元),它们与投入资金t(万元)的关系有经验公式P=3 ![]() ,Q=t.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(万元).求:
,Q=t.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(万元).求:
(1)经营甲、乙两种商品的总利润y(万元)关于x的函数表达式;
(2)怎样将资金分配给甲、乙两种商品,能使得总利润y达到最大值,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为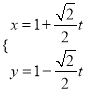 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 点的直角坐标为
点的直角坐标为![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() ,点
,点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 上.
上.
(1)求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 由无数对相互垂直的直线
由无数对相互垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com