
 =
=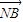 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得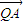 •
•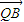 =0,并说明理由.
=0,并说明理由.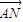 =
=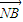 求得x2和x1的关系式,代入方程入①②求得k,则直线的方程可得.
求得x2和x1的关系式,代入方程入①②求得k,则直线的方程可得. 有公共点,先看直线l的斜率不存在,则以AB为直径的圆为(x-2)2+y2=9,可知其与直线x=
有公共点,先看直线l的斜率不存在,则以AB为直径的圆为(x-2)2+y2=9,可知其与直线x= 相交;再看斜率存在时设出直线的方程,利用焦点坐标和离心率求得|AB|的表达式,设以AB为直径的圆的圆心为S,点S到直径x=
相交;再看斜率存在时设出直线的方程,利用焦点坐标和离心率求得|AB|的表达式,设以AB为直径的圆的圆心为S,点S到直径x= 的距离为d,则d可求,d-
的距离为d,则d可求,d-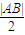 判断出结果小于0,推断出d<
判断出结果小于0,推断出d<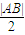 ,进而可知直线x=
,进而可知直线x= 与圆S相交,最后综合可得答案.
与圆S相交,最后综合可得答案.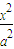 -
-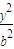 =1(a>0,b>0)则a=1,c=2,
=1(a>0,b>0)则a=1,c=2,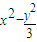 =1,(x≥1).
=1,(x≥1).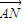 =
=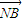 ,故l的斜率存在,设l的方程为y=k(x-2),
,故l的斜率存在,设l的方程为y=k(x-2),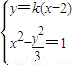 得(3-k2)x2+4k2x-4k2-3=0,又设A(x1,y1),B(x2,y2),则
得(3-k2)x2+4k2x-4k2-3=0,又设A(x1,y1),B(x2,y2),则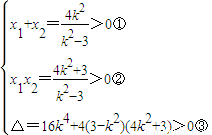
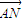 =
=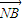 ∴2(2-x1,-y1)=(x2-2,y2)
∴2(2-x1,-y1)=(x2-2,y2)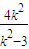 =6-x1,
=6-x1,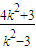 =x1(6-2x1)
=x1(6-2x1)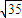 ,故所求直线l的方程为:y=±
,故所求直线l的方程为:y=±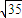 (x-2);
(x-2); 有公共点
有公共点 相交;若直线l的斜率存在,则设直线l的方程为y=k(x-2),A(x1,y1),B(x2,y2)
相交;若直线l的斜率存在,则设直线l的方程为y=k(x-2),A(x1,y1),B(x2,y2)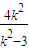 ,又N(2,0)为双曲线的右焦点,双曲线的离心率e=2,
,又N(2,0)为双曲线的右焦点,双曲线的离心率e=2,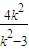 -2=
-2=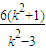
 的距离为d,则d=
的距离为d,则d=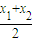 -
- =
=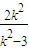 -
- =
=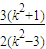
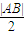 =
= -
-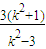 =-
=-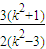
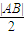 <0即d<
<0即d<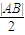 ,即直线x=
,即直线x= 与圆S相交.
与圆S相交. 相交;
相交; 上存在一点Q(实际上存在两点)使得
上存在一点Q(实际上存在两点)使得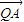 •
•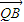 =0
=0

 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
| AN |
| NB |
| 1 |
| 2 |
| QA |
| QB |
查看答案和解析>>
科目:高中数学 来源:0103 模拟题 题型:解答题
 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。 ,求直线
,求直线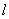 的方程;
的方程;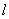 的任意一确定的位置,在直线x=
的任意一确定的位置,在直线x= 上是否存在一点Q,使得
上是否存在一点Q,使得 ,并说明理由。
,并说明理由。 查看答案和解析>>
科目:高中数学 来源:2011年河北省衡水市冀州中学高考数学一模试卷(理科)(解析版) 题型:解答题
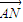 =
=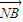 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得 •
•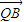 =0,并说明理由.
=0,并说明理由.查看答案和解析>>
科目:高中数学 来源:2011年高三数学单元检测:圆锥曲线(2)(解析版) 题型:解答题
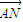 =
=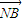 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得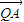 •
•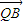 =0,并说明理由.
=0,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com