
如下图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.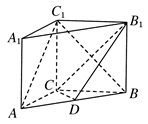
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
(1)先证明AC⊥平面BCC1B1,再根据性质即可证明
(2)先证明DE∥AC1,再根据线面平行的判定定理证明
(3)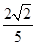
解析试题分析:(1)在直三棱柱ABC-A1B1C1中,底面三边长AC=3,BC=4,AB=5,
∴AC⊥BC.又∵C1C⊥AC.∴AC⊥平面BCC1B1.
∵BC1?平面BCC1B,∴AC⊥BC1.
(2)设CB1与C1B的交点为E,连接DE,又四边形BCC1B1为正方形.
∵D是AB的中点,E是BC1的中点,∴DE∥AC1.
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(3)∵DE∥AC1,∴∠CED为AC1与B1C所成的角.
在△CED中,ED=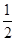 AC1=
AC1=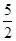 ,CD=
,CD=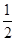 AB=
AB=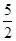 ,CE=
,CE=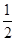 CB1=2
CB1=2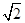 ,
,
∴cos∠CED= =
=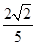 .
.
∴异面直线AC1与B1C所成角的余弦值为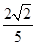 .
.
考点:本小题主要考查线线垂直、线面平行的判定和两条异面直线所成的角的计算,考查学生的空间想象能力和运算求解能力.
点评:解决此类问题,要准确应用相应的判定定理和性质定理并注意相互转化,求解两条异面直线的夹角问题时,要注意夹角的取值范围.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
(理科)(本小题满分12分)如图分别是正三棱台ABC-A1B1C1的直观图和正视图,O,O1分别是上下底面的中心,E是BC中点.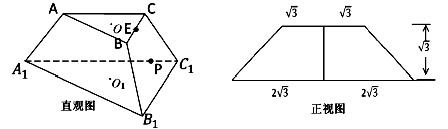
(1)求正三棱台ABC-A1B1C1的体积;
(2)求平面EA1B1与平面A1B1C1的夹角的余弦;
(3)若P是棱A1C1上一点,求CP+PB1的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本题共有2个小题,第(1)小题满分6分,第(2)小题满分6分.
如图,已知正四棱柱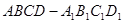 的底面边长是
的底面边长是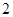 ,体积是
,体积是 ,
, 分别是棱
分别是棱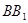 、
、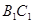 的中点.
的中点.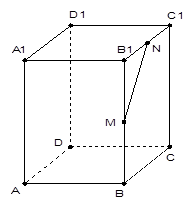
(1)求直线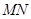 与平面
与平面 所成的角(结果用反三角函数表示);
所成的角(结果用反三角函数表示);
(2)求过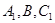 的平面与该正四棱柱所截得的多面体
的平面与该正四棱柱所截得的多面体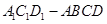 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知四棱柱 的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,
的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱, ,
,
E是侧棱AA1的中点,求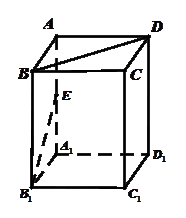
(1)求异面直线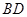 与B1E所成角的大小;
与B1E所成角的大小;
(2)求四面体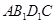 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正方形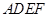 与梯形
与梯形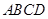 所在的平面互相垂直,
所在的平面互相垂直,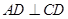 ,
, ∥
∥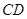 ,
,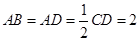 ,点
,点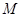 在线段
在线段 上.
上.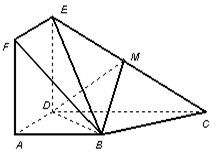
(I)当点 为
为 中点时,求证:
中点时,求证: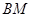 ∥平面
∥平面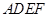 ;
;
(II)当平面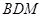 与平面
与平面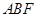 所成锐二面角的余弦值为
所成锐二面角的余弦值为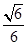 时,求三棱锥
时,求三棱锥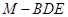 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com