
【题目】已知在![]() 中,
中,![]() ,
,![]() 点在直线
点在直线![]() 上,若
上,若![]() 的面积为10,求
的面积为10,求![]() 点的坐标.
点的坐标.
【答案】(方法Ⅰ)解:设点C到直线AB的距离为d
由题意知:![]() ………………………………………2分
………………………………………2分
4分 |
4分 |
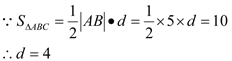 直线AB的方程为:
直线AB的方程为:![]() ,即
,即![]() ……………………………6分
……………………………6分
![]() C点在直线3x-y+3=0上,设C
C点在直线3x-y+3=0上,设C![]()
10分 |
10分 |
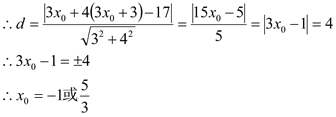
![]() C点的坐标为:
C点的坐标为:![]() 或
或![]() ……………………………………………………12分
……………………………………………………12分
(方法Ⅱ)解:设点C到直线AB的距离为d
由题意知:![]() ………………………………………2分
………………………………………2分
4分 |
4分 |
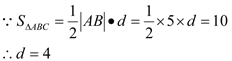 直线AB的方程为:
直线AB的方程为:![]() ,即
,即![]() …………………………6分
…………………………6分
设C点的坐标为![]()
由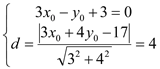 ]
]
10分 |
10分 |
解得: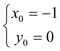 或
或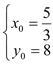
![]() C点的坐标为:
C点的坐标为:![]() 或
或![]() ……………………………………………………12分
……………………………………………………12分
]
【解析】
分析:设点![]() 坐标为
坐标为![]() ,求出
,求出![]() 的距离,利用三角形的面积求出
的距离,利用三角形的面积求出![]() 到
到![]() 的距离,利用点到直线的距离公式以及点在直线上,列出关于
的距离,利用点到直线的距离公式以及点在直线上,列出关于![]() 的方程组,可求出
的方程组,可求出![]() 的坐标.
的坐标.
详解:设点![]() 坐标为
坐标为![]() ,由题意,得
,由题意,得
![]() .
.
因为![]() ,所以
,所以![]() .(
.(![]() 为点
为点![]() 到直线
到直线![]() 的距离)
的距离)
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由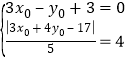 ,
,
解得![]() 或
或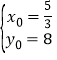 .
.
所以点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A.命题“若 ![]() ,则
,则 ![]() ”的逆命题为“若
”的逆命题为“若 ![]() ,则
,则 ![]() ”
”
B.对于命题 ![]() ,使得
,使得 ![]() ,则
,则 ![]() ,则
,则 ![]()
C.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
D.若 ![]() 为假命题,则
为假命题,则 ![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知圆
中,已知圆 ![]() ,点
,点 ![]() ,点
,点 ![]() ,以B为圆心,
,以B为圆心, ![]() 为半径作圆,交圆C于点P,且
为半径作圆,交圆C于点P,且 ![]() 的平分线交线段CP于点Q.
的平分线交线段CP于点Q.
(1)当a变化时,点Q始终在某圆锥曲线 ![]() 上运动,求曲线
上运动,求曲线 ![]() 的方程;
的方程;
(2)已知直线l过点C,且与曲线 ![]() 交于M,N两点,记
交于M,N两点,记 ![]() 面积为
面积为 ![]() ,
, ![]() 面积为
面积为 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从参加某次高中英语竞赛的学生中抽出100名,将其成绩整理后,绘制频率分布直方图(如图所示).其中样本数据分组区间为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
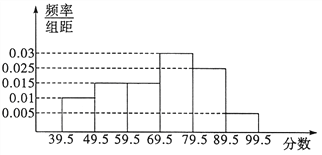
(Ⅰ)试求图中![]() 的值,并计算区间
的值,并计算区间![]() 上的样本数据的频率和频数;
上的样本数据的频率和频数;
(Ⅱ)试估计这次英语竞赛成绩的众数、中位数及平均成绩(结果精确到![]() ).
).
注:同一组数据用该组区间的中点值作为代表
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,是否存在折叠后的线段
,是否存在折叠后的线段![]() 上存在一点
上存在一点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(![]() )求三棱锥
)求三棱锥![]() 的体积的最大值,并求此时点
的体积的最大值,并求此时点![]() 到平面
到平面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
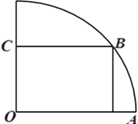
【题目】如图,在半径为3![]() 的
的![]() 圆形(
圆形(![]() 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料![]() ,其中点
,其中点![]() 在圆弧上,点
在圆弧上,点![]() 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮![]() 卷成一个以
卷成一个以![]() 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长![]() ,圆柱的体积为
,圆柱的体积为![]() .
.
(1)写出体积![]() 关于
关于![]() 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当![]() 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积![]() 最大?最大体积是多少?(圆柱体积公式:
最大?最大体积是多少?(圆柱体积公式: ![]() ,
, ![]() 为圆柱的底面积,
为圆柱的底面积, ![]() 为圆柱的高)
为圆柱的高)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com