
Ϊ��Ѱ������ �к�,�ҹ���ѩ���š��ƿ�����2014��3��26�մӸۿ�
�к�,�ҹ���ѩ���š��ƿ�����2014��3��26�մӸۿ� �������ر�ƫ��
�������ر�ƫ�� �ǵ�����
�ǵ�����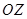 �����У����ڸۿڱ�ƫ��
�����У����ڸۿڱ�ƫ�� �ǵķ�������һ�����ƿ����������ʵ�С��
�ǵķ�������һ�����ƿ����������ʵ�С�� ��
�� �����
�����
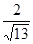 .��ָ�Ӳ���Ҫ��������λ�ڸۿ�
.��ָ�Ӳ���Ҫ��������λ�ڸۿ� ����
����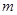 �����
����� ���IJ�������������
���IJ�����������С�� װ�ϲ������ʹ����ƿ������ô���
װ�ϲ������ʹ����ƿ������ô���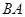 ����ȫ���Ͽƿ���������
����ȫ���Ͽƿ��������� �������������㵱�������еĺ����뺣����
�������������㵱�������еĺ����뺣����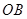 Χ�ɵ�������
Χ�ɵ�������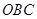 �����
�����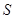 ��Сʱ�����ֲ�����������.
��Сʱ�����ֲ�����������.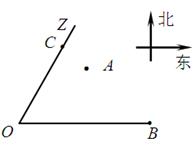
��1����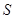 ����
����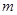 �ĺ�����ϵʽ
�ĺ�����ϵʽ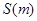 ��
��
��2��Ӧ����λ�ڸۿ��������ٺ��ﴦ�IJ�����ֻ�������������ţ�
��1��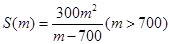 ����2��1400��
����2��1400��
���������������1��������֪������������Ϊ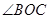 �ǹ̶��ģ���
�ǹ̶��ģ��� Ҳ�Dz��䣬ֱ��
Ҳ�Dz��䣬ֱ��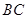 ����
���� ��Ҫ��
��Ҫ��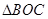 �������Сֵ��������֪�����������ý����������⣬��
�������Сֵ��������֪�����������ý����������⣬�� Ϊ����ԭ�㣬����Ϊ
Ϊ����ԭ�㣬����Ϊ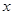 �����ᣬ����Ϊ
�����ᣬ����Ϊ �������ᣬ����ֱ������ϵ����ɵ�ֱ��
�������ᣬ����ֱ������ϵ����ɵ�ֱ��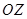 �ķ���Ϊ
�ķ���Ϊ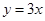 ����
���� ����Ϊ
����Ϊ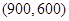 �����е�
�����е� ����Ϊ
����Ϊ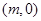 ���ɵ�ֱ��
���ɵ�ֱ��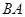 ���̣�����ֱ��
���̣�����ֱ��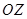 �Ľ���
�Ľ��� ������ɽ�ã���
������ɽ�ã��� ������Ҫ��ı���ʽ�Ϳɵã���2���ڣ�1�������ϣ�
������Ҫ��ı���ʽ�Ϳɵã���2���ڣ�1�������ϣ�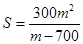 ������Сֵ���ѷ�ʽ�ķ��ӷ�ĸͬʱ����
������Сֵ���ѷ�ʽ�ķ��ӷ�ĸͬʱ����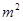 ����
����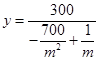 ����ĸ�ǹ���
����ĸ�ǹ���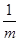 �Ķ��κ�������ֵ����.
�Ķ��κ�������ֵ����.
�����������1����O��Ϊԭ�㣬�����ķ���Ϊy����������ֱ������ϵ�� ��1�֣�
��ֱ��OZ�ķ���Ϊ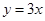 �����A��x0��y0������
�����A��x0��y0������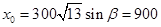 ��
��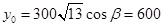 ����A��900��600���� ��3�֣�
����A��900��600���� ��3�֣�
��B��m��0������ֱ��AB�ķ���Ϊ��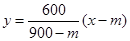 �� ��4�֣�
�� ��4�֣�
�ɴ˵õ�C������Ϊ��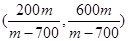 �� ��6�֣�
�� ��6�֣� ��8�֣�
��8�֣�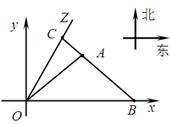
��2���ɣ�1��֪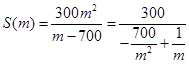 ��10�֣�
��10�֣�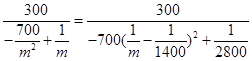 ��12�֣�
��12�֣�
���Ե�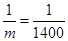 ����
����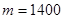 ʱ��
ʱ��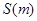 ��С��
����
������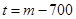 ����
����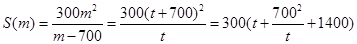
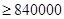 �����ҽ���
�����ҽ���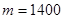 ʱ��
ʱ��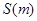 ��С��
����
������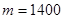 ���ﴦ�Ĵ�ֻʱ��������������. ��14�֣�
���ﴦ�Ĵ�ֻʱ��������������. ��14�֣�
���㣺��������Ӧ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�������һ����װ�У���ͼ��ʾ�� �DZ߳�Ϊ
�DZ߳�Ϊ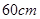 ��������ӲֽƬ����ȥ��Ӱ������ʾ���ĸ�ȫ�ȵĵ���ֱ�������Σ�������������ʹ��
��������ӲֽƬ����ȥ��Ӱ������ʾ���ĸ�ȫ�ȵĵ���ֱ�������Σ�������������ʹ�� �ĸ����غ���ͼ�еĵ�P�������γ�һ������������״�İ�װ�У�
�ĸ����غ���ͼ�еĵ�P�������γ�һ������������״�İ�װ�У� ��
�� ���DZ���ȥ�ĵ���ֱ��������б�ߵ������˵㣬��
���DZ���ȥ�ĵ���ֱ��������б�ߵ������˵㣬�� ��
��
��1���������Ҫ���װ�в���� �������
������� Ӧȡ��ֵ��
Ӧȡ��ֵ��
��2���������Ҫ���װ���ݻ� �������
������� Ӧȡ��ֵ���������ʱ��װ�еĸ������߳��ı�ֵ��
Ӧȡ��ֵ���������ʱ��װ�еĸ������߳��ı�ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����
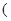 ����
����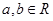 ������
������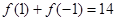 .
.
��1����� ��ֵ�����ͳ���
��ֵ�����ͳ��� �IJ�ͬȡֵ���ۺ���
�IJ�ͬȡֵ���ۺ��� ��ż�ԣ�
��ż�ԣ�
��2���� ������
������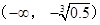 �ϵ����ݼ�����
�ϵ����ݼ����� ����Сֵ��
����Сֵ��
��3���ڣ�2���������£��� ȡ��Сֵʱ��֤����
ȡ��Сֵʱ��֤���� ǡ��һ�����
ǡ��һ�����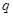 �Ҵ��ڵ���������������
�Ҵ��ڵ���������������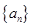 ��ʹ��
��ʹ��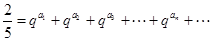 ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2011•��������1����֪����f��x��=lnx��x+1��x�ʣ�0��+�ޣ�������f��x�������ֵ��
��2����a1��b1��k=1��2����n����Ϊ������֤����
����a1b1+a2b2+��anbn��b1+b2+��bn����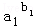
 ��
��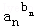 ��1��
��1��
����b1+b2+��bn=1���� ��
��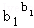
 ��
��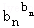 ��b12+b22+��+bn2��
��b12+b22+��+bn2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�����x���� ����0
����0
��f(x)����Сֵm��ʾ��a�ĺ���m=g(a);
�Ƿ����ʵ��a,ʹf(x)>0�� �Ϻ������
�Ϻ������
�Ƿ����ʵ��a��ʹ����f(x) �� �ϵ��������������ڣ�д�����е�a��ɵļ��ϣ��������ڣ�˵������.
�ϵ��������������ڣ�д�����е�a��ɵļ��ϣ��������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����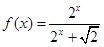 ��
��
��1������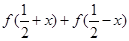 ��ֵ��
��ֵ��
��2�������� �IJ���ʽ��
�IJ���ʽ��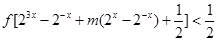 ������
������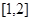 ���н⣬��ʵ��
���н⣬��ʵ��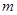 ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��˾�н��Ȼ�����״�Ļ�̳��ͼ��ʾ�����Ȼ��滨̳�����Ե� ΪԲ�ĵ�����ͬ��Բ��
ΪԲ�ĵ�����ͬ��Բ�� ����
���� �Լ������߶�
�Լ������߶� ��
�� Χ�ɵķ��ͼ�Σ���̳����ܳ�Ϊ30�ף����д�Բ��
Χ�ɵķ��ͼ�Σ���̳����ܳ�Ϊ30�ף����д�Բ�� ����Բ�İ뾶Ϊ10�ף���СԲ��
����Բ�İ뾶Ϊ10�ף���СԲ�� ����Բ�İ뾶Ϊ
����Բ�İ뾶Ϊ �ף�
�ף� ����Բ�Ľ�Ϊ
����Բ�Ľ�Ϊ ���ȣ�
���ȣ�
��1���� ����
���� �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���ڶԻ�̳�ı�Ե����װ��ʱ����֪�����߶ε�װ�η���Ϊ4Ԫ/�ף��������߲��ֵ�װ�η���Ϊ9Ԫ/�ף��軨̳�������װ���ܷ��õı�Ϊ ����
���� Ϊ��ֵʱ��
Ϊ��ֵʱ�� ȡ�����ֵ��
ȡ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
���ں���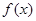 �����ڶ��������ʵ��
�����ڶ��������ʵ��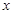 ������
������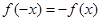 �����
�����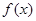 Ϊ���ֲ��溯������
Ϊ���ֲ��溯������
��1����֪���κ���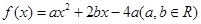 �����ж�
�����ж�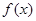 �Ƿ�Ϊ���ֲ��溯��������˵�����ɣ�
�Ƿ�Ϊ���ֲ��溯��������˵�����ɣ�
��2����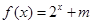 �Ƕ�����
�Ƕ�����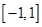 �ϵġ��ֲ��溯��������ʵ��
�ϵġ��ֲ��溯��������ʵ��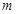 ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����f(x)��lg(ax��bx)(a>1>b>0)��
(1)����y��f(x)�Ķ�����
(2)�ں���y��f(x)��ͼ�����Ƿ���ڲ�ͬ�����㣬ʹ���������ֱ��ƽ����x�
(3)��a��b����ʲô��ϵʱ��f(x)������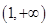 �Ϻ�ȡ��ֵ��
�Ϻ�ȡ��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com