
【题目】已知二次函数![]()
(1)若函数![]() 是偶函数,求实数
是偶函数,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 且任意
且任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 在
在![]() 上的最小值
上的最小值![]() 。
。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)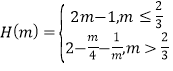 .
.
【解析】
(1)偶函数f(﹣x)=f(x)x2+mx+1=x2﹣mx+1,可求实数m的取值范围;
(2)m∈[﹣1,3],g(x)=f(x)+(2m﹣1)x﹣9=x2+(m﹣1)x﹣8≤0恒成立![]() ,解之即得实数x的取值范围;
,解之即得实数x的取值范围;
(3)若函数h(x)=f(x)﹣(1﹣m)x2+2x=mx2+(2﹣m)x+1,分![]() 、m
、m![]() 、当m<0及m=0四类讨论,即可求得函数y=h(x)在x∈[﹣1,1]的最小值H(m).
、当m<0及m=0四类讨论,即可求得函数y=h(x)在x∈[﹣1,1]的最小值H(m).
(1)函数![]() 是偶函数,
是偶函数,![]()
![]() ,
,
![]()
(2)![]()
![]() 都有
都有![]() 恒成立
恒成立
![]() ,
,![]()
![]() 实数
实数![]() 的取值范围是
的取值范围是![]()
(3)![]()
①当![]() 时,函数
时,函数![]() 对称轴
对称轴![]()
![]() 函数
函数![]() 在
在![]() 上的最小值
上的最小值![]()
②当![]() 时,函数
时,函数![]() 对称轴
对称轴![]()
![]() 函数
函数![]() 在
在![]() 上的最小值
上的最小值
![]()
③当![]() 时,函数
时,函数![]() 的对称轴
的对称轴![]()
![]() 函数
函数![]() 在
在![]() 上的最小值
上的最小值![]()
④当![]() 时,函数
时,函数![]()
![]() 函数
函数![]() 在
在![]() 上的最小值
上的最小值![]()
综上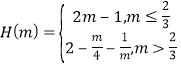


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】有以下4个命题:
①若 ![]() ,则a﹣c>b﹣d; ②若a≠0,b≠0,则
,则a﹣c>b﹣d; ②若a≠0,b≠0,则 ![]() ;③两条直线平行的充要条件是它们的斜率相等; ④过点(x0 , y0)与圆x2+y2=r2相切的直线方程是x0x+y0y=r2 .
;③两条直线平行的充要条件是它们的斜率相等; ④过点(x0 , y0)与圆x2+y2=r2相切的直线方程是x0x+y0y=r2 .
其中错误命题的序号是 . (把你认为错误的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程 ![]() =1表示的曲线为C,给出以下四个判断:
=1表示的曲线为C,给出以下四个判断:
①当1<t<4时,曲线C表示椭圆;
②当t>4或t<1时曲线C表示双曲线;
③若曲线C表示焦点在x轴上的椭圆,则1<t< ![]() ;
;
④若曲线C表示焦点在x轴上的双曲线,则t>4,
其中判断正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点B与点A(﹣1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于﹣ ![]() .
.
(1)求动点P的轨迹方程;
(2)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() ,且
,且 ![]() . (Ⅰ)试将y表示为x的函数f(x),并求f(x)的单调递增区间;
. (Ⅰ)试将y表示为x的函数f(x),并求f(x)的单调递增区间;
(Ⅱ)已知a、b、c分别为△ABC的三个内角A、B、C对应的边长,若 ![]() ,且
,且 ![]() ,a+b=6,求△ABC的面积.
,a+b=6,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE= ![]() .
. 
(1)求证:AB⊥平面BCF;
(2)求直线AE与平面BDE所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,经过村庄A有两条夹角60°为的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).记∠AMN=θ. 
(1)将AN,AM用含θ的关系式表示出来;
(2)如何设计(即AN,AM为多长时),使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离AP最大)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中说法正确的是( )
A.命题“p∨q为真”是命题“p∧q为真”的必要条件
B.向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角
的夹角为锐角
C.若am2≤bm2 , 则a≤b
D.“?x0∈R,x02﹣x0≤0”的否定是“?x∈R,x2﹣x≥0”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com