
【题目】设函数![]() .
.
(1)若![]() ,
,![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)若![]() 是函数
是函数![]() 的一个极值点,试求出
的一个极值点,试求出![]() 关于
关于![]() 的关系式(即用
的关系式(即用![]() 表示
表示![]() ),并确定
),并确定![]() 的单调区间;(提示:应注意对
的单调区间;(提示:应注意对![]() 的取值范围进行讨论)
的取值范围进行讨论)
(3)在(2)的条件下,设![]() ,函数
,函数![]() ,若存在
,若存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ,见解析; (3)
,见解析; (3)![]() .
.
【解析】
(1)求出导函数的根,判断根左右两边导函数的符号,得到函数的单调性,据极大值极小值的定义求出极值;(2)据极值点处的导函数值为0得到a,b的关系;代入导函数中求出导函数的两根,讨论两根的大小;判断根左右两边导函数的符号,据导函数与单调性的关系求出单调区间;(3)据函数的单调性求出两个函数的值域,求出函数值的最小距离,最小距离小于1求出a的范围
(1)∵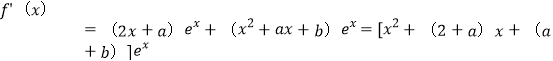
当![]() ,
,![]() 时,
时,![]() 则
则![]()
令![]() 得
得![]() ,∵
,∵![]() ∴
∴![]() ,解得
,解得![]() ,
,![]()
∵当![]() 时,
时,![]() ,当
,当![]() 时
时![]() ,当
,当![]() 时
时![]()
∴当![]() 时,函数
时,函数![]() 有极大值,
有极大值,![]() ,
,
当![]() 时,函数
时,函数![]() 有极小值,
有极小值,![]() .
.
(2)由(1)知![]()
∵![]() 是函数
是函数![]() 的一个极值点
的一个极值点
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
则![]()
令![]() ,得
,得![]() 或
或![]()
∵![]() 是极值点,∴
是极值点,∴![]() ,即
,即![]()
当![]() 即
即![]() 时,由
时,由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
当![]() 即
即![]() 时,由
时,由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
综上可知:当![]() 时,单调递增区间为
时,单调递增区间为![]() 和
和![]() ,递减区间为
,递减区间为![]()
当![]() 时,单调递增区间为
时,单调递增区间为![]() 和
和![]() ,递减区间为
,递减区间为![]()
(3)由(2)知,当![]() 时,
时,![]() 在区间
在区间![]() 上的单调递减,在区间
上的单调递减,在区间![]() 上单调递增,
上单调递增,
∴函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
又∵![]() ,
,![]() ,
,
∴函数![]() 在区间
在区间![]() 上的值域是
上的值域是![]() ,即
,即![]()
又![]() 在区间
在区间![]() 上是增函数,
上是增函数,
且它在区间![]() 上的值域是
上的值域是![]()
∵![]() ,
,
∴存在![]() 使得
使得![]()
成立只须仅须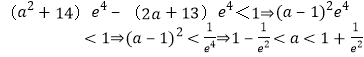 .
.


科目:高中数学 来源: 题型:
【题目】某学校高二年级的第二学期,因某学科的任课教师王老师调动工作,于是更换了另一名教师赵老师继任.第二学期结束后从全学年的该门课的学生考试成绩中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如下:
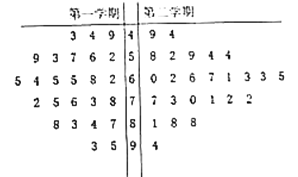
学校秉持均衡发展、素质教育的办学理念,对教师的教学成绩实行绩效考核,绩效考核方案规定:每个学期的学生成绩中与其中位数相差在![]() 范围内(含
范围内(含![]() )的为合格,此时相应的给教师赋分为1分;与中位数之差大于10的为优秀,此时相应的给教师赋分为2分;与中位数之差小于-10的为不合格,此时相应的给教师赋分为-1分.
)的为合格,此时相应的给教师赋分为1分;与中位数之差大于10的为优秀,此时相应的给教师赋分为2分;与中位数之差小于-10的为不合格,此时相应的给教师赋分为-1分.
(Ⅰ)问王老师和赵老师的教学绩效考核平均成绩哪个大?
(Ⅱ)是否有![]() 的把握认为“学生成绩取得优秀与更换老师有关”.
的把握认为“学生成绩取得优秀与更换老师有关”.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2019年的冬令营考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| 35 | 0.350 |
第3组 |
| 10 | 0.100 |
第4组 |
| 20 | 0.200 |
第5组 |
| 30 | 0.300 |
合计 | 100 | 1.00 | |
(1)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(2)在(1)的前提下,高校决定在这6名学生中,随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被A考官测试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知![]() ,且2an+1=an+1(n∈N*).
,且2an+1=an+1(n∈N*).
(1)求证:数列{an-1}是等比数列;
(2)若bn=nan,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,楔形几何体![]() 由一个三棱柱截去部分后所得,底面
由一个三棱柱截去部分后所得,底面![]() 侧面
侧面![]() ,
,![]() ,楔面
,楔面![]() 是边长为2的正三角形,点
是边长为2的正三角形,点![]() 在侧面
在侧面![]() 的射影是矩形
的射影是矩形![]() 的中心
的中心![]() ,点
,点![]() 在
在![]() 上,且
上,且![]()
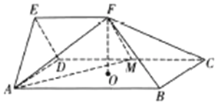
(1)证明:![]() 平面
平面![]() ;
;
(2)求楔面![]() 与侧面
与侧面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图,长方体![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,过点
的中点,过点![]() 的平面
的平面![]() 与平面
与平面![]() 平行,且与长方体的面相交,交线围成一个几何图形.
平行,且与长方体的面相交,交线围成一个几何图形.
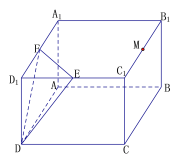
(1)在图中画出这个几何图形,并求这个几何图形的面积(画图说出作法,不用说明理由);
(2)求证:![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com