
【题目】已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c,且2acos A=ccos B+bcos C.
(Ⅰ)求A;
(Ⅱ)若b2+c2=7,求△ABC的面积.
【答案】解:(Ⅰ)因为2acos A=ccos B+bcos C,则由正弦定理得:2sin Acos A=sin Ccos B+sin Bcos C, 所以2sin Acos A=sin(B+C)=sin A,
又0<A<π,
所以sin A≠0,从而2cos A=1,cos A= ![]() ,
,
故A= ![]() ;
;
(Ⅱ)由A= ![]() 知sin A=
知sin A= ![]() ,而△ABC的外接圆半径为1,
,而△ABC的外接圆半径为1,
故由正弦定理可得a=2sin A= ![]() ,
,
再由余弦定理a2=b2+c2﹣2bccos A,
可得bc=b2+c2﹣a2=7﹣3=4,
∴S△ABC= ![]() bcsin A=
bcsin A= ![]()
【解析】(Ⅰ)根据正弦定理和以及两角和正弦公式即可得到cos A= ![]() ,问题得以解决,(Ⅱ)根据正弦定理和余弦定理可得bc的值,即可求出三角形的面积.
,问题得以解决,(Ⅱ)根据正弦定理和余弦定理可得bc的值,即可求出三角形的面积.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() 、
、 ![]() ,短轴两个端点为
,短轴两个端点为 ![]() 、
、 ![]() ,且四边形
,且四边形 ![]() 是边长为2的正方形.
是边长为2的正方形.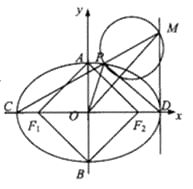
(1)求椭圆的方程;
(2)若 ![]() 、
、 ![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 ![]() 满足
满足 ![]() ,连接
,连接 ![]() ,交椭圆于点
,交椭圆于点 ![]() .证明:
.证明: ![]() 为定值.
为定值.
(3)在(2)的条件下,试问 ![]() 轴上是否存异于点
轴上是否存异于点 ![]() 的定点
的定点 ![]() ,使得以
,使得以 ![]() 为直径的圆恒过直线
为直径的圆恒过直线 ![]() 、
、 ![]() 的交点,若存在,求出点
的交点,若存在,求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)= ![]() +bx(a≠0)
+bx(a≠0)
(Ⅰ)若a=﹣2时,函数h(x)=f(x)﹣g(x)在其定义域内是增函数,求b的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设φ(x)=e2x+bex , x∈[0,ln2],求函数φ(x)的最小值;
(Ⅲ)设函数f(x)的图象C1与函数g(x)的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形 ABCD 中,对角线 AC 与 BD 相交于一点 O,∠A=60°,将△BDC 沿着 BD 折起得△BDC',连结 AC'.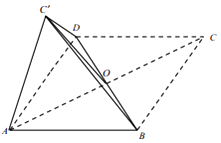
(Ⅰ)求证:平面 AOC'⊥平面 ABD;
(Ⅱ)若点 C'在平面 ABD 上的投影恰好是△ABD 的重心,求直线 CD 与底面 ADC'所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=2,b1=4,且 2bn=an+an+1 , an+12=bnbn+1 .
(Ⅰ)求 a 2 , a3 , a4 及b2 , b3 , b4;
(Ⅱ)猜想{an},{bn} 的通项公式,并证明你的结论;
(Ⅲ)证明:对所有的 n∈N* , ![]()
![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查中小学课外使用互联网的情况,教育部向华东、华北、华南和西部地区60所中小学发出问卷![]() 份,
份, ![]() 名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
(1)要从这![]() 名中小学中用分层抽样的方法抽取
名中小学中用分层抽样的方法抽取![]() 名中小学生进一步调查,则在
名中小学生进一步调查,则在![]() (小时)时间段内应抽出的人数是多少?
(小时)时间段内应抽出的人数是多少?
(2)若希望![]() 的中小学生每天使用互联网时间不少于
的中小学生每天使用互联网时间不少于![]() (小时),请估计
(小时),请估计![]() 的值,并说明理由.
的值,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax(a>0,a≠1)在区间[﹣1,2]上的最大值为8,最小值为m.若函数g(x)=(3﹣10m) ![]() 是单调增函数,则a= .
是单调增函数,则a= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC=a,AC=b,且a,b是方程![]() 的两根,2cos(A+B)=1.
的两根,2cos(A+B)=1.
(1)求∠C的度数;
(2)求AB的长;
(3)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,点D是BC的中点.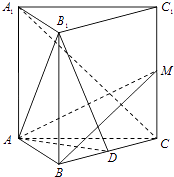
(1)求证:A1C∥平面AB1D;
(2)设M为棱CC1的点,且满足BM⊥B1D,求证:平面AB1D⊥平面ABM.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com