
【题目】已知曲线 (
(![]() 为参数),曲线
为参数),曲线![]() ,将
,将![]() 的横坐标伸长为原来的2倍,纵坐标缩短为原来的
的横坐标伸长为原来的2倍,纵坐标缩短为原来的![]() 得到曲线
得到曲线![]() .
.
(1)求曲线![]() 的普通方程,曲线
的普通方程,曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 为曲线
为曲线![]() 上的任意一点,
上的任意一点,![]() 为曲线
为曲线![]() 上的任意一点,求线段
上的任意一点,求线段![]() 的最小值,并求此时的
的最小值,并求此时的![]() 的坐标;
的坐标;
(3)过(2)中求出的点![]() 做一直线
做一直线![]() ,交曲线
,交曲线![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值(
面积的最大值(![]() 为直角坐标系的坐标原点),并求出此时直线
为直角坐标系的坐标原点),并求出此时直线![]() 的方程.
的方程.
【答案】(1)曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]() ;(2)最小值为
;(2)最小值为![]() ,此时
,此时![]() ;(3)最大值为
;(3)最大值为![]() ,此时
,此时![]() .
.
【解析】
(1)通过变换求出曲线![]() 的参数方程然后化为普通方程,利用极坐标与直角坐标的关系,求解曲线
的参数方程然后化为普通方程,利用极坐标与直角坐标的关系,求解曲线![]() 的直角坐标方程;(2)由题意线段
的直角坐标方程;(2)由题意线段![]() 的最小值,转为圆的圆心到直线的距离减去半径,利用直线的垂直关系,即可求此时的P的坐标.(3)写出三角形的面积公式即可得到最大值,并得到圆心O到直线l的距离,设出直线l的方程,利用圆心到直线的距离公式进行计算即可得到答案.
的最小值,转为圆的圆心到直线的距离减去半径,利用直线的垂直关系,即可求此时的P的坐标.(3)写出三角形的面积公式即可得到最大值,并得到圆心O到直线l的距离,设出直线l的方程,利用圆心到直线的距离公式进行计算即可得到答案.
(1)曲线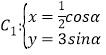 (
(![]() 为参数),将
为参数),将![]() 的横坐标伸长为原来的2倍,
的横坐标伸长为原来的2倍,
纵坐标缩短为原来的![]() 得到曲线
得到曲线![]() ,化为普通方程为
,化为普通方程为![]() ,
,
曲线![]() ,即
,即![]() ,
,
可得直角坐标方程为![]() .
.
(2)设![]() ,则线段
,则线段![]() 的最小值为点P到直线
的最小值为点P到直线![]() 的距离.
的距离.
转为圆心到直线的距离减去半径,![]() ,
,
直线![]() 的斜率为-1,所以直线PQ的斜率为1,直线PQ方程为y=x,
的斜率为-1,所以直线PQ的斜率为1,直线PQ方程为y=x,
联立![]() 解得Q(1,1).
解得Q(1,1).
(3)由题意可得![]() ,
,
当![]() ,即
,即![]() 时取到面积的最大值
时取到面积的最大值![]() ,
,
此时可知圆心O到直线l的距离为![]() ,
,
由题意可得直线l的斜率肯定存在并设为k,
则直线l的方程为y-1=k(x-1),即kx-y-k+1=0,
圆心到直线l的距离![]() ,解得
,解得![]() ,
,
所以直线l的方程为:![]()


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中, ![]() ,
, ![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中:
翻折过程中:

①![]() 是定值;②点
是定值;②点![]() 在某个球面上运动;
在某个球面上运动;
③存在某个位置,使![]() ;④存在某个位置,使
;④存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若曲线C上任意一点与直线![]() 上任意一点的距离都大于1,则称曲线C远离”直线
上任意一点的距离都大于1,则称曲线C远离”直线![]() ,在下列曲线中,“远离”直线
,在下列曲线中,“远离”直线![]() :y=2x的曲线有___________(写出所有符合条件的曲线的编号)
:y=2x的曲线有___________(写出所有符合条件的曲线的编号)
①曲线C:![]() ;②曲线C:
;②曲线C:![]() ;③曲线C:
;③曲线C:![]() ;
;
④曲线C:![]() ;⑤曲线C:
;⑤曲线C:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是梯形,AD∥BC,∠BAD=90°,四边形CC1D1D为矩形,已知AB⊥BC1,AD=4,AB=2,BC=1.

(I)求证:BC1∥平面ADD1;
(II)若DD1=2,求平面AC1D1与平面ADD1所成的锐二面角的余弦值;
(III)设P为线段C1D上的一个动点(端点除外),判断直线BC1与直线CP能否垂直?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1642年,帕斯卡发明了一种可以进行十进制加减法的机械计算机![]() 年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念
年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念![]() 之后,人们对进位制的效率问题进行了深入的研究
之后,人们对进位制的效率问题进行了深入的研究![]() 研究方法如下:对于正整数
研究方法如下:对于正整数![]() ,
,![]() ,我们准备
,我们准备![]() 张不同的卡片,其中写有数字0,1,…,
张不同的卡片,其中写有数字0,1,…,![]() 的卡片各有
的卡片各有![]() 张
张![]() 如果用这些卡片表示
如果用这些卡片表示![]() 位
位![]() 进制数,通过不同的卡片组合,这些卡片可以表示
进制数,通过不同的卡片组合,这些卡片可以表示![]() 个不同的整数
个不同的整数![]() 例如
例如![]() ,
,![]() 时,我们可以表示出
时,我们可以表示出![]() 共
共![]() 个不同的整数
个不同的整数![]() 假设卡片的总数
假设卡片的总数![]() 为一个定值,那么
为一个定值,那么![]() 进制的效率最高则意味着
进制的效率最高则意味着![]() 张卡片所表示的不同整数的个数
张卡片所表示的不同整数的个数![]() 最大
最大![]() 根据上述研究方法,几进制的效率最高?
根据上述研究方法,几进制的效率最高?![]()
![]()
A. 二进制 B. 三进制 C. 十进制 D. 十六进制
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在推导很多三角恒等变换公式时,我们可以利用平面向量的有关知识来研究,在一定程度上可以简化推理过程.如我们就可以利用平面向量来推导两角差的余弦公式:![]()
具体过程如下:
如图,在平面直角坐标系![]() 内作单位圆O,以
内作单位圆O,以![]() 为始边作角
为始边作角![]() .它们的终边与单位圆O的交点分别为A,B.
.它们的终边与单位圆O的交点分别为A,B.

则![]()
由向量数量积的坐标表示,有:
![]()
设![]() 的夹角为θ,则
的夹角为θ,则
![]()
另一方面,由图3.1—3(1)可知,![]() ;由图可知,
;由图可知,

![]() .于是
.于是![]() .
.
所以![]() ,也有
,也有![]() ,
,
所以,对于任意角![]() 有:
有:![]() (
(![]() )
)
此公式给出了任意角![]() 的正弦、余弦值与其差角
的正弦、余弦值与其差角![]() 的余弦值之间的关系,称为差角的余弦公式,简记作
的余弦值之间的关系,称为差角的余弦公式,简记作![]() .
.
有了公式![]() 以后,我们只要知道
以后,我们只要知道![]() 的值,就可以求得
的值,就可以求得![]() 的值了.
的值了.
阅读以上材料,利用下图单位圆及相关数据(图中M是AB的中点),采取类似方法(用其他方法解答正确同等给分)解决下列问题:
(1)判断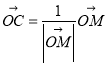 是否正确?(不需要证明)
是否正确?(不需要证明)
(2)证明:![]()
(3)利用以上结论求函数![]() 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有一特色酒店由一些完全相同的帐篷构成.每座帐篷的体积为![]() 立方米,且分上下两层,其中上层是半径为
立方米,且分上下两层,其中上层是半径为![]() (单位:米)的半球体,下层是半径为
(单位:米)的半球体,下层是半径为![]() 米,高为
米,高为![]() 米的圆柱体(如图).经测算,上层半球体部分每平方米建造费用为2千元,下方圆柱体的侧面、隔层和地面三个部分平均每平方米建造费用为3千元,设每座帐篷的建造费用为
米的圆柱体(如图).经测算,上层半球体部分每平方米建造费用为2千元,下方圆柱体的侧面、隔层和地面三个部分平均每平方米建造费用为3千元,设每座帐篷的建造费用为![]() 千元.
千元.
参考公式:球的体积![]() ,球的表面积
,球的表面积![]() ,其中
,其中![]() 为球的半径.
为球的半径.

(1)求![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)当半径![]() 为何值时,每座帐篷的建造费用最小,并求出最小值.
为何值时,每座帐篷的建造费用最小,并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com