练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知曲C的极坐标方程ρ=2sinθ，设直线L的参数方程 ，（t为参数）设直线L与x轴的交点M，N是曲线C上一动点，求|MN|的最大值 ．

    【答案】
    【解析】解：∵曲线C的极坐标方程ρ=2sinθ，化成普通方程： x2+y2﹣2y=0，即x2+（y﹣1）2=1
    ∴曲线C表示以点P（0，1）为圆心，半径为1的圆
    ∵直L的参数方程是：
    ∴直L的普通方程是：4x+3y﹣8=0
    ∴可得L与x轴的交点M坐标为（2，0）
    ∴
    由此可得曲C上一动点N到M的最大距离等于
    故答案为：
    首先将曲线C化成普通方程，得出它是以P（0，1）为圆心半径为1的圆，然后将直线L化成普通方程，得出它与x轴的交点M的坐标，最后用两个点之间的距离公式得出PM的距离，从而得出曲C上一动点N到M的最大距离．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知在△ABC中，角A、B、C的对边分别为a、b、c，且满足cos2A﹣cos2B=2cos（ ﹣A）cos（ +A）．
    （1）求角B的值；
    （2）若b= 且b≤a，求2a﹣c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足：a1= ，an=an﹣12+an﹣1（n≥2且n∈N）．
    （Ⅰ）求a2 ， a3；并证明：2 ﹣ ≤an≤ 3 ；
    （Ⅱ）设数列{an2}的前n项和为An ， 数列{ }的前n项和为Bn ， 证明： = an+1 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（ax+1）ex﹣（a+1）x﹣1．
    （1）求y=f（x）在（0，f（0））处的切线方程；
    （2）若x＞0时，不等式f（x）＞0恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-5：不等式选讲]
    设函数f（x）=|x﹣4|，g（x）=|2x+1|．
    （1）解不等式f（x）＜g（x）；
    （2）若2f（x）+g（x）＞ax对任意的实数x恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知等边中， ， 分别为， 边的中点， 为的中点， 为边上一点，且，将沿折到的位置，使平面平面.

    （Ⅰ）求证：平面平面；

    （Ⅱ）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知长方体ABCD-A1B1C1D1中，底面ABCD为正方形，AB=4，AA1=2，点E1在棱C1D1上，且D1E1=3。

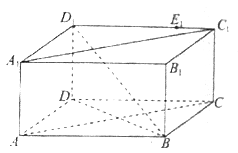
    （I）在棱CD上确定一点E，使得直线EE1∥平面D1DB，并写出证明过程；

    （II）求证：平面A1ACC1⊥平面D1DB；

    （III）若动点F在正方形ABCD内，且AF=2，请说明点F的轨迹，试求E1F长度的最小值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AB∥DC，DA⊥AB，AB=AP=2，DA=DC=1，E为PC上一点，且PE= PC．

    （Ⅰ）求PE的长；
    （Ⅱ）求证：AE⊥平面PBC；
    （Ⅲ）求二面角B﹣AE﹣D的度数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C所对边分别是a，b，c，若sin（A﹣B）= sinAcosB﹣ sinBcosA．
    （1）求证：A=B；
    （2）若A= ，a= ，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案