
【题目】自平面上一点O引两条射线OA,OB,P在OA上运动,Q在OB上运动且保持| ![]() |为定值2
|为定值2 ![]() (P,Q不与O重合).已知∠AOB=120°,
(P,Q不与O重合).已知∠AOB=120°,
(I)PQ的中点M的轨迹是的一部分(不需写具体方程);
(II)N是线段PQ上任﹣点,若|OM|=1,则 ![]()
![]() 的取值范围是 .
的取值范围是 .
【答案】椭圆;[1﹣ ![]() ,1+
,1+ ![]() ]
]
【解析】解:(I)以OB为x轴,过O垂直于OB的直线为y轴,|OQ|=a,|OP|=b,则P(﹣ ![]() ,
, ![]() b),Q(a,0),
b),Q(a,0),
∴M( ![]() ,
, ![]() b),
b),
设M(x,y),则x= ![]() ,y=
,y= ![]() b,
b,
∴a=2x+ ![]() y,b=
y,b= ![]() y
y
由余弦定理可得a2+b2+ab=8,
∴3x2+4 ![]() xy+7y2=6,
xy+7y2=6,
∴PQ的中点M的轨迹是椭圆的一部分;
(II)∵| ![]() |为定值2
|为定值2 ![]() ,|OM|=1,
,|OM|=1,
∴a2+b2=6,
∵a2+b2+ab=8,
∴ab=2,
∴a= ![]() ,b=
,b= ![]() ,
,
∴P(﹣ ![]() ,
, ![]() ),Q(
),Q( ![]() ,0),M(
,0),M( ![]() ,
, ![]() ),
),
∴ ![]() =1﹣
=1﹣ ![]() ,
, ![]() =1+
=1+ ![]() ,
, ![]() =1
=1
∴ ![]()
![]() 的取值范围是[1﹣
的取值范围是[1﹣ ![]() ,1+
,1+ ![]() ].
].
所以答案是:椭圆;[1﹣ ![]() ,1+
,1+ ![]() ].
].


科目:高中数学 来源: 题型:
【题目】输入x,求函数y=![]() 的值的程序框图如图C17所示.
的值的程序框图如图C17所示.
(1)指出程序框图中的错误之处并写出正确的算法步骤.
(2)重新绘制程序框图,并回答下面提出的问题.
①要使输出的值为7,则输入的x的值应为多少?
②要使输出的值为正数,则输入的x应满足什么条件?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,P为双曲线 ![]() ﹣y2=1(a>0)上一点,过P作两条渐近线的平行线交点分别为A,B,若平行四边形OAPB的面积为
﹣y2=1(a>0)上一点,过P作两条渐近线的平行线交点分别为A,B,若平行四边形OAPB的面积为 ![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )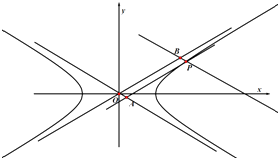
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +y2=1与直线l:y=kx+m相交于E、F两不同点,且直线l与圆O:x2+y2=
+y2=1与直线l:y=kx+m相交于E、F两不同点,且直线l与圆O:x2+y2= ![]() 相切于点W(O为坐标原点).
相切于点W(O为坐标原点).
(1)证明:OE⊥OF;
(2)设λ= ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,在同一个坐标系中,
,在同一个坐标系中,![]() 及
及![]() 的部分图象如图所示,则( ).
的部分图象如图所示,则( ).

A. 当![]() 时,
时,![]() 取得最大值 B. 当
取得最大值 B. 当![]() 时,
时,![]() 取得最大值
取得最大值
C. 当![]() 时,
时,![]() 取得最小值 D. 当
取得最小值 D. 当![]() 时,
时,![]() 取得最小值
取得最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人相约于下午1:00~2:00之间到某车站乘公共汽车外出,他们到达车站的时间是随机的.设在下午1:00~2:00之间该车站有四班公共汽车开出,开车时间分别是1:15,1:30,1:45,2:00.求他们在下述情况下乘同一班车的概率:
(1)约定见车就乘;
(2)约定最多等一班车.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+ax+b,a,b∈R.
(1)若2a+b=4,证明:|f(x)|在区间[0,4]上的最大值M(a)≥12;
(2)存在实数a,使得当x∈[0,b]时,1≤f(x)≤10恒成立,求实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的右准线方程为
的右准线方程为![]() ,又离心率为
,又离心率为![]() ,椭圆的左顶点为
,椭圆的左顶点为![]() ,上顶点为
,上顶点为![]() ,点
,点![]() 为椭圆上异于
为椭圆上异于![]() 任意一点.
任意一点.
(1)求椭圆的方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() =1的离心率e=
=1的离心率e= ![]() ,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.
,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若椭圆C1的方程为 ![]() =1(m>n>0),椭圆C2的方程为
=1(m>n>0),椭圆C2的方程为 ![]() =λ(λ>0,且λ≠1),则称椭圆C2是椭圆C1的λ倍相似椭圆.已知椭圆C2是椭圆C的3倍相似椭圆.若过椭圆C上动点P的切线l交椭圆C2于A,B两点,O为坐标原点,试证明当切线l变化时|PA|=|PB|并研究△OAB面积的变化情况.
=λ(λ>0,且λ≠1),则称椭圆C2是椭圆C1的λ倍相似椭圆.已知椭圆C2是椭圆C的3倍相似椭圆.若过椭圆C上动点P的切线l交椭圆C2于A,B两点,O为坐标原点,试证明当切线l变化时|PA|=|PB|并研究△OAB面积的变化情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com