
【题目】设函数f(x)是(﹣∞,0)∪(0,+∞)上的偶函数,x>0时f(x)=x﹣ ![]() ,求x<0时f(x)的表达式,判断f(x)在(﹣∞,0)上的单调性,并用定义给出证明.
,求x<0时f(x)的表达式,判断f(x)在(﹣∞,0)上的单调性,并用定义给出证明.
【答案】解:∵函数f(x)是(﹣∞,0)∪(0,+∞)上的偶函数,
x>0时f(x)=x﹣ ![]() ,
,
∴x<0时,f(x)=(﹣x)﹣ ![]() =﹣x+
=﹣x+ ![]() ,
,
f(x)在(﹣∞,0)上的单调递减,证明如下:
在(﹣∞,0)上任取x1 , x2 , 令x1<x2 ,
则f(x1)﹣f(x2)=(﹣x1+ ![]() )﹣(﹣x2+
)﹣(﹣x2+ ![]() )=(x2﹣x1)+
)=(x2﹣x1)+ ![]() =(x2﹣x1)(1﹣
=(x2﹣x1)(1﹣ ![]() ),
),
∵x1 , x2∈(﹣∞,0),x1<x2 ,
∴f(x1)﹣f(x2)=(x2﹣x1)(1﹣ ![]() )>0,
)>0,
∴f(x)在(﹣∞,0)上的单调递减
【解析】由已知得x<0时,f(x)=(﹣x)﹣ ![]() =﹣x+
=﹣x+ ![]() ,f(x)在(﹣∞,0)上的单调递减,利用定义法能进行证明.
,f(x)在(﹣∞,0)上的单调递减,利用定义法能进行证明.
【考点精析】本题主要考查了函数单调性的判断方法的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在10件产品中,有2件一等品,4件二等品,4件三等品,从这10件产品中任取3件,求
(1)取出的3件产品中一等品件数X的分布列和数学期望;
(2)取出的3件产品中至多有1件一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ﹣
﹣ ![]()
(1)证明函数f(x)是奇函数;
(2)证明函数f(x)在(﹣∞,+∞)内是增函数;
(3)求函数f(x)在[1,2]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作直线
作直线![]() ,
, ![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() 是直线
是直线![]() 上两个不同的点,且
上两个不同的点,且![]() 的内切圆方程为
的内切圆方程为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数),直线l经过点P(1,1),倾斜角
(θ为参数),直线l经过点P(1,1),倾斜角 ![]() ,
,
(1)写出直线l的参数方程;
(2)设l与圆C相交于两点A,B,求点P到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 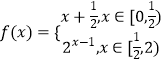 ,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com