
已知两点 及
及 ,点
,点 在以
在以 、
、 为焦点的椭圆
为焦点的椭圆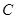 上,且
上,且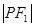 、
、 、
、 构成等差数列.
构成等差数列.

(1)求椭圆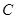 的方程;
的方程;
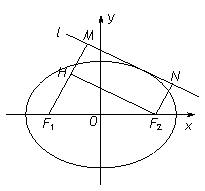
(2)如图7,动直线 与椭圆
与椭圆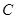 有且仅有一个公共点,点
有且仅有一个公共点,点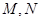 是直线
是直线 上的两点,且
上的两点,且 ,
,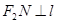 . 求四边形
. 求四边形 面积
面积 的最大值.
的最大值.
(1)椭圆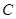 的方程为
的方程为 .(2)以四边形
.(2)以四边形 的面积
的面积 的最大值为
的最大值为 。
。
【解析】
试题分析:(1)依题意,设椭圆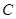 的方程为
的方程为 .
.

 构成等差数列,
构成等差数列,

 ,
,  .
.
又 ,
, .
.
 椭圆
椭圆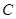 的方程为
的方程为 . 4分
. 4分
(2) 将直线 的方程
的方程 代入椭圆
代入椭圆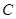 的方程
的方程 中,得
中,得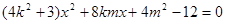 . 5分
. 5分
由直线 与椭圆
与椭圆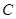 仅有一个公共点知,
仅有一个公共点知,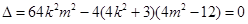 ,
,
化简得: . 7分
. 7分
设 ,
, , 9分
, 9分
(法一)当 时,设直线
时,设直线 的倾斜角为
的倾斜角为 ,
,
则 ,
,
 ,
,

 , 11分
, 11分

 ,
, 当
当 时,
时, ,
, ,
, .
.
当 时,四边形
时,四边形 是矩形,
是矩形,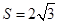 . 13分
. 13分
所以四边形 面积
面积 的最大值为
的最大值为 . 14分
. 14分
(法二)
 ,
,
 .
.

 .
.
四边形 的面积
的面积
 , 11分
, 11分
 . 13分
. 13分
当且仅当 时,
时, ,故
,故 .
.
所以四边形 的面积
的面积 的最大值为
的最大值为 . 14分
. 14分
考点:本题主要考查等差数列,椭圆标准方程,直线与椭圆的位置关系,面积计算。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆、标准方程时,主要运用了椭圆的几何性质。解题过程中,运用等差数列的基础知识求得了a,b,c的关系。


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2013-2014学年云南省部分名校高三12月联考理科数学试卷(解析版) 题型:解答题
已知两点 及
及 ,点
,点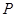 在以
在以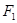 、
、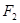 为焦点的椭圆
为焦点的椭圆 上,且
上,且 、
、 、
、 构成等差数列.
构成等差数列.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)如图,动直线 与椭圆
与椭圆 有且仅有一个公共点,点
有且仅有一个公共点,点 是直线
是直线 上的两点,且
上的两点,且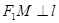 ,
,
 .
求四边形
.
求四边形 面积
面积 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年云南省部分名校高三12月联考文科数学试卷(解析版) 题型:解答题
已知两点 及
及 ,点
,点 在以
在以 、
、 为焦点的椭圆
为焦点的椭圆 上,且
上,且 、
、 、
、 构成等差数列.
构成等差数列.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)如图,动直线 与椭圆
与椭圆 有且仅有一个公共点,点
有且仅有一个公共点,点 是直线
是直线 上的两点,且
上的两点,且 ,
, .
求四边形
.
求四边形 面积
面积 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市鄞州区高三5月适应性考试理科数学试卷(解析版) 题型:解答题
已知两点 及
及 ,点
,点 在以
在以 、
、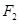 为焦点的椭圆
为焦点的椭圆 上,且
上,且 、
、 、
、 构成等差数列.
构成等差数列.

(1)求椭圆 的方程;
的方程;
(2)如图,动直线 与椭圆
与椭圆 有且仅有一个公共点,点
有且仅有一个公共点,点 是直线上的两点,且
是直线上的两点,且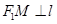 ,
, . 求四边形
. 求四边形 面积
面积 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两点![]() 及
及![]() ,点
,点![]() 在以
在以![]() 、
、![]() 为焦点的椭圆
为焦点的椭圆![]() 上,且
上,且![]() 、
、![]() 、
、![]() 构成等差数列.
构成等差数列.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,
有且仅有一个公共点,
点![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() ,
,![]() .
.
求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com