
【题目】已知椭圆![]() 的短轴端点到右焦点
的短轴端点到右焦点![]() 的距离为2.
的距离为2.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() ,若
,若![]() ,
, ![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1) ![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(Ⅰ)利用椭圆的几何要素间的关系进行求解;(Ⅱ)联立直线和椭圆的方程,得到关于![]() 或
或![]() 的一元二次方程,利用根与系数的关系和平面向量的线性运算进行证明.
的一元二次方程,利用根与系数的关系和平面向量的线性运算进行证明.
试题解析:(Ⅰ)由题意有: ![]() ,且
,且![]() ,
,
所以![]() ,
, ![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)由题意直线![]() 过点
过点![]() ,且斜率存在,设方程为
,且斜率存在,设方程为![]() ,
,
将![]() 代人得
代人得![]() 点坐标为
点坐标为![]() ,
,
由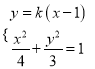 ,消元得
,消元得![]() ,
,
设![]() ,
, ![]() ,则
,则![]() 且
且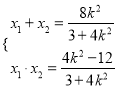 ,
,
方法一:因为![]() ,所以
,所以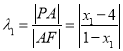 .
.
同理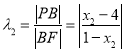 ,且
,且![]() 与
与![]() 异号,
异号,
所以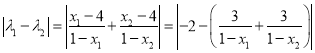

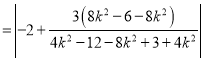
![]() .
.
所以, ![]() 为定值
为定值![]() .
.
方法二:由题意,当![]() 时, (若:不妨设
时, (若:不妨设![]() ,加一分)
,加一分)
有![]() ,且
,且![]() ,
,
所以![]() ,且
,且![]()
所以![]() ,同理
,同理![]() .
.
从而![]()
![]()
![]()
![]() .
.
当![]() 时,同理可得
时,同理可得![]() .
.
所以, ![]() 为定值
为定值![]() .
.
方法三:由题意直线![]() 过点
过点![]() ,设方程为
,设方程为![]()
![]() ,
,
将![]() 代人得
代人得![]() 点坐标为
点坐标为![]() ,
,
由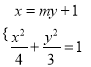 消元得
消元得![]() ,
,
设![]() ,
, ![]() ,则
,则![]() 且
且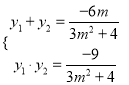 ,
,
因为![]() ,所以
,所以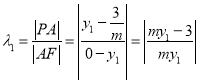 .
.
同理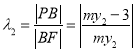 ,且
,且![]() 与
与![]() 异号,
异号,
所以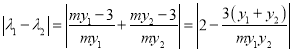
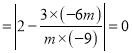 .
.
又当直线![]() 与
与![]() 轴重合时,
轴重合时, ![]() ,
,
所以, ![]() 为定值
为定值![]() .
.


科目:高中数学 来源: 题型:
【题目】2017年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如下表:
评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
评分类型 | D | C | B | A |
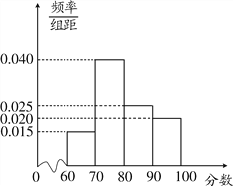 考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
(Ⅰ)评分类型为A的商业连锁店有多少家;
(Ⅱ)现从评分类型为A,D的所有商业连锁店中随机抽取两家做分析,求这两家来自同一评分类型的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定两个长度为1的平面向量 ![]() 和
和 ![]() ,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧
,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧 ![]() 上变动.若
上变动.若 ![]() ,其中x,y∈R,试求x+y的最大值.
,其中x,y∈R,试求x+y的最大值. 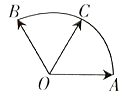
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为预防H1N1病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如表:
A组 | B组 | C组 | |
疫苗有效 | 673 | x | y |
疫苗无效 | 77 | 90 | z |
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求x的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知y≥465,z≥25,求不能通过测试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论: ①已知函数f(x)是定义在R上的奇函数,若f(﹣1)=2,f(﹣3)=﹣1,则f(3)<f(﹣1);
②函数y=log ![]() (x2﹣2x)的单调递增减区间是(﹣∞,0);
(x2﹣2x)的单调递增减区间是(﹣∞,0);
③已知函数f(x)是奇函数,当x≥0时,f(x)=x2 , 则当x<0时,f(x)=﹣x2;
④若函数y=f(x)的图象与函数y=ex的图象关于直线y=x对称,则对任意实数x,y都有f(xy)=f(x)+f(y).
则正确结论的序号是(请将所有正确结论的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
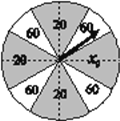
【题目】某大型超市拟对店庆当天购物满![]() 元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
(Ⅰ)若![]() ,求顾客转动一次转盘获得
,求顾客转动一次转盘获得![]() 元代金券的概率;
元代金券的概率;
(Ⅱ)某顾客可以连续转动两次转盘并获得相应奖励,当![]() 时,求该顾客第一次获得代金券的面额不低于第二次获得代金券的面额的概率;
时,求该顾客第一次获得代金券的面额不低于第二次获得代金券的面额的概率;
(Ⅲ)记顾客每次转动转盘获得代金券的面额为![]() ,当
,当![]() 取何值时,
取何值时, ![]() 的方差最小?
的方差最小?
(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对营销人员有如下规定:
①年销售额![]() (万元)在8万元以下,没有奖金;
(万元)在8万元以下,没有奖金;
②年销售额![]() (万元),
(万元), ![]() 时,奖金为
时,奖金为![]() 万元,且
万元,且![]() ,
, ![]() ,且年销售额越大,奖金越多;
,且年销售额越大,奖金越多;
③年销售额超过64万元,按年销售额的10%发奖金.
(1)求奖金y关于x的函数解析式;
(2)若某营销人员争取奖金![]() (万元),则年销售额
(万元),则年销售额![]() (万元)在什么范围内?
(万元)在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)(ω>0,||< ![]() ,x∈R)的部分图象如图所示,则函数表达式为( )
,x∈R)的部分图象如图所示,则函数表达式为( ) 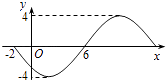
A.y=﹣4sin( ![]() )
)
B.y=4sin( ![]() )
)
C.y=﹣4sin( ![]() )
)
D.y=4sin( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,
中, ![]() 为坐标原点,曲线
为坐标原点,曲线![]() :
: 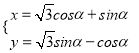 (
(![]() 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,取相同单位长度的极坐标系,直线
轴的正半轴为极轴,取相同单位长度的极坐标系,直线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)曲线![]() 上恰好存在三个不同的点到直线
上恰好存在三个不同的点到直线![]() 的距离相等,分别求出这三个点的极坐标.
的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com