
| |||||||||||
(1) |
解析:设点M的坐标为(x,y),由 由 所以,动点M的轨迹C是以(0,0)为顶点,(1,0)为焦点的抛物线(除去原点). |
(2) |
设直线l:y=k(x+1),其中k≠0,代入y2=4x得k2x2+2(k2-2)x十k2=0. ① 设A(x1,y1),B(x2,y2),则x1、x2是方程①的两个实根. 所以x1+x2=- 则线段AB的中点坐标为( 令y=0,解得x0= 因为△ABE为正三角形,所以点E( 而|AB|= = 所以 解得k=± |


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
| AF |
| FB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足
已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
| 1 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
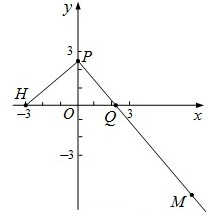 (2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足
(2009•卢湾区二模)如图,已知点H(-3,0),动点P在y轴上,点Q在x轴上,其横坐标不小于零,点M在直线PQ上,且满足| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
| x2 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com