
【题目】已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
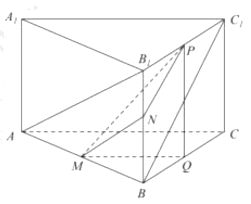
【解析】解:如图所示,设M、N、P分别为AB,BB1和B1C1的中点,
则AB1、BC1夹角为MN和NP夹角或其补角
(因异面直线所成角为(0, ![]() ]),
]),
可知MN= ![]() AB1=
AB1= ![]() ,
,
NP= ![]() BC1=
BC1= ![]() ;
;
作BC中点Q,则△PQM为直角三角形;
∵PQ=1,MQ= ![]() AC,
AC,
△ABC中,由余弦定理得
AC2=AB2+BC2﹣2ABBCcos∠ABC
=4+1﹣2×2×1×(﹣ ![]() )
)
=7,
∴AC= ![]() ,
,
∴MQ= ![]() ;
;
在△MQP中,MP= ![]() =
= ![]() ;
;
在△PMN中,由余弦定理得
cos∠MNP= ![]() =
= 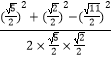 =﹣
=﹣ ![]() ;
;
又异面直线所成角的范围是(0, ![]() ],
],
∴AB1与BC1所成角的余弦值为 ![]() .
.
【考点精析】掌握异面直线及其所成的角是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】有一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示.为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有![]() 米.若行车道总宽度
米.若行车道总宽度![]() 为
为![]() 米.
米.
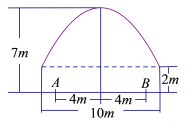
(1)计算车辆通过隧道时的限制高度;
(2)现有一辆载重汽车宽![]() 米,高
米,高![]() 米,试判断该车能否安全通过隧道?
米,试判断该车能否安全通过隧道?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x<2},B={x|3﹣2x>0},则( )
A.A∩B={x|x< ![]() }
}
B.A∩B=?
C.A∪B={x|x< ![]() }
}
D.AUB=R
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏
B.3盏
C.5盏
D.9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2 ![]() .
.
(Ⅰ)求cosB;
(Ⅱ)若a+c=6,△ABC面积为2,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= ![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
(Ⅰ)证明:直线CE∥平面PAB;
(Ⅱ)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知S2=6,an+1=4Sn+1,n∈N* .
(1)求通项an;
(2)设bn=an﹣n﹣4,求数列{|bn|}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com