
(本题满分12分)
若 ,且
,且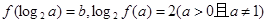 ,
,
(1)求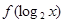 的最小值及相应 x的值;
的最小值及相应 x的值;
(2)若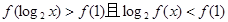 ,求x的取值范围.
,求x的取值范围.
(1)f (log2x)有最小值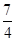 ,x=
,x=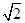 (2)0<x<1
(2)0<x<1
解析试题分析:(1)∵f (x)=x2-x+b,∴f (log2a)= (log2a)2-log2a+b=b,∴log2a=1∴a=2. ……2分
又∵log2f(a)=2,f(a)=4.∴a2-a+b=4,∴b=2.∴f (x)=x2-x+2 ……4分
∴f (log2x)= (log2x)2-log2x+2= (log2x- )2+
)2+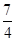 ,
,
∴当log2x= ,即x=
,即x=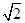 时,f (log2x)有最小值
时,f (log2x)有最小值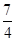 . ……6分
. ……6分
(2)由题意知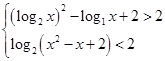 ……8分
……8分
∴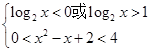 ……10分
……10分
∴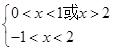 ∴ 0<x<1 ……12分
∴ 0<x<1 ……12分
考点:函数求解析式及解不等式
点评:求函数解析式主要用到的是待定系数法,整道题目在求解过程中多处涉及到了对数运算需结合对数函数性质考虑,整体来看难度不大,需分析求解时认真细心


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
(10分)为了预防流感,某学校对教室用药熏消毒法进行消毒。已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为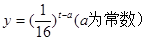 ,如图所示。
,如图所示。
(1)请写出从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室。那么,从药物释放开始,至少需要经过多少小时后,学生才能回到教室。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)已知函数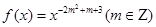 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数.
(1)求 的值,并确定
的值,并确定 的解析式;
的解析式;
(2)若 且
且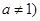 ,是否存在实数
,是否存在实数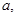 使
使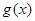 在区间
在区间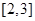 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知函数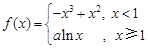 ,其中
,其中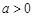
(Ⅰ)求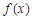 在
在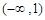 上的单调区间;
上的单调区间;
(Ⅱ)求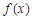 在
在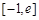 (
(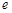 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;
(III)对任意给定的正实数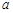 ,曲线
,曲线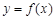 上是否存在两点
上是否存在两点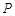 、
、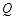 ,使得
,使得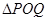 是以原点
是以原点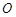 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在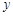 轴上?
轴上?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分15分)
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: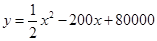 ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数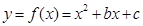 的图象过点(1,13),图像关于直线
的图象过点(1,13),图像关于直线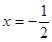 对称。
对称。
(1)求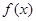 的解析式。
的解析式。
(2)已知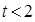 ,
,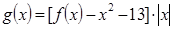 ,
,
① 若函数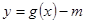 的零点有三个,求实数
的零点有三个,求实数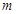 的取值范围;
的取值范围;
②求函数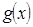 在[
在[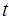 ,2]上的最小值。
,2]上的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分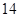 分)
分)
若函数 在定义域
在定义域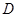 内某区间
内某区间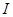 上是增函数,而
上是增函数,而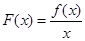 在
在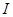 上是减函数,
上是减函数,
则称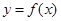 在
在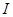 上是“弱增函数”
上是“弱增函数”
(1)请分别判断 =
=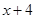 ,
,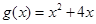 在
在 是否是“弱增函数”,
是否是“弱增函数”,
并简要说明理由;
(2)证明函数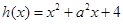 (
( 是常数且
是常数且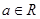 )在
)在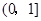 上是“弱增函数”.
上是“弱增函数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com