
【题目】已知函数f(x)=(x-k)ex.
(1)求f(x)的单调区间;
(2)求f(x)在区间[0,1]上的最小值.
【答案】(1)f(x)的单调递减区间是(-∞,k-1);单调递增区间是(k-1,+∞);(2)见解析.
【解析】
(1)求导,令导数等于零,解方程,跟据f′(x)随x的变化情况即可求出函数的单调区间;(2)根据(1),对k﹣1是否在区间[0,1]内进行讨论,从而求得f(x)在区间[0,1]上的最小值.
(1)由题意知f′(x)=(x-k+1)ex.
令f′(x)=0,得x=k-1.
f(x)与f′(x)随x的变化情况如下:

所以,f(x)的单调递减区间是(-∞,k-1);单调递增区间是(k-1,+∞).
(2)当k-1≤0,即k≤1时,f(x)在[0,1]上单调递增,所以f(x)在区间[0,1]上的最小值为f(0)=-k;
当0<k-1<1,即1<k<2时,f(x)在[0,k-1]上单调递减,在[k-1,1]上单调递增,所以f(x)在区间[0,1]上的最小值为f(k-1)=-ek-1;
当k-1≥1,即k≥2时,f(x)在[0,1]上单调递减,
所以f(x)在区间[0,1]上的最小值为f(1)=(1-k)e.
综上,当k≤1时,f(x)在[0,1]上的最小值为
f(0)=-k;
当1<k<2时,f(x)在[0,1]上的最小值为
f(k-1)=-ek-1;
当k≥2时,f(x)在[0,1]上的最小值为f(1)=(1-k)e.


科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() ),在
),在![]() 上既无最大值,也无最小值,且
上既无最大值,也无最小值,且![]() ,则下列结论成立的是( )
,则下列结论成立的是( )
A.若![]() 对任意
对任意![]() ,则
,则![]()
B.![]() 的图象关于点
的图象关于点![]() 中心对称
中心对称
C.函数![]() 的单调减区间为
的单调减区间为![]()
D.函数![]() 的图象相邻两条对称轴之间的距离是
的图象相邻两条对称轴之间的距离是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《数书九章》是中国南宋时期杰出数学家秦九韶的著作,其中在卷五“三斜求积”中提出了已知三角形三边![]() 、
、![]() 、
、![]() ,求面积的公式,这与古希腊的海伦公式完全等价,其求法是“以小斜冥并大斜冥减中斜冥,余半之,自乘于上,以小斜冥乘大斜冥减上,余四约之,为实.一为从隅,开平方得积”若把以上这段文字写出公式,即若
,求面积的公式,这与古希腊的海伦公式完全等价,其求法是“以小斜冥并大斜冥减中斜冥,余半之,自乘于上,以小斜冥乘大斜冥减上,余四约之,为实.一为从隅,开平方得积”若把以上这段文字写出公式,即若![]() ,则
,则![]() .
.
(1)已知![]() 的三边
的三边![]() ,
,![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() 的面积
的面积![]() .
.
(2)若![]() ,
,![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
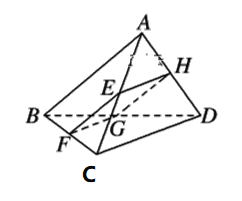
(1)求证:AB∥平面EFGH
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形,SA=SB= SC=2,AB=2,设S、A、B、C四点均在以O为球心的某个球面上。则点O到平面ABC的距离为________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com