
(本小题满分12分)已知函数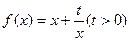 和点
和点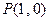 ,过点
,过点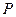 作曲线
作曲线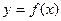 的两条切线
的两条切线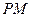 、
、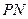 ,切点分别为
,切点分别为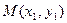 、
、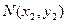 .
.
(1)求证: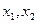 为关于
为关于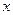 的方程
的方程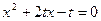 的两根;
的两根;
(2)设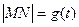 ,求函数
,求函数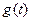 的表达式;
的表达式;
(3)在(2)的条件下,若在区间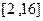 内总存在
内总存在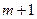 个实数
个实数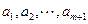 (可以相同),使得不等式
(可以相同),使得不等式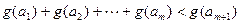 成立,求
成立,求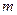 的最大值.
的最大值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
如图,有一块半椭圆形钢板,其长半轴长为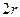 ,短半轴长为
,短半轴长为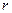 ,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记
,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记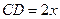 ,梯形面积为S.
,梯形面积为S.
(1) 求面积S以
求面积S以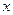 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(2)求面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分15分)某经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位:
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果的费用为y(元)(不计返程费用),将y表示成速度v的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题11分)如图,矩形ABCD中,AB=6,BC=2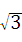 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;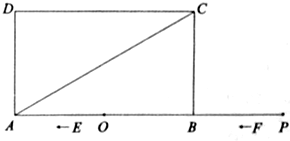
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列四个判断:
①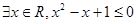 ;
;
②已知随机变量X服从正态分布N(3, ),P(X≤6)=0.72,则P(X≤0)=0.28;
),P(X≤6)=0.72,则P(X≤0)=0.28;
③已知 的展开式的各项系数和为32,则展开式中x项的系数为20;
的展开式的各项系数和为32,则展开式中x项的系数为20;
④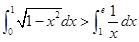
其中正确的个数有:
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商家经销一种销售成本 为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况,
为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况,
(1)设销售单价为每千克x元,月销售利润 为y元,求y与x的函数关系式;
为y元,求y与x的函数关系式;
商店想在月销售成本不超过10000元的情况下,使得月销售利润不少于8000元,销售单价应定为多少元时,利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)若定义在 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件:
①对任意实数 均有
均有 成立;
成立;
②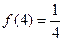 ;
;
③当 时,都有
时,都有 成立。
成立。
(1)求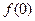 ,
, 的值;
的值;
(2)求证: 为
为 上的增函数
上的增函数
(3)求解关于 的不等式
的不等式 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com