
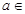 R,函数
R,函数 (x∈R).
(x∈R). 时,求函数f(x)的单调递增区间;
时,求函数f(x)的单调递增区间; 的取值范围;若不能,请说明理由;
的取值范围;若不能,请说明理由; 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.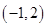 ;(2)当
;(2)当 时, 函数f(x)在R上单调递减;(3)
时, 函数f(x)在R上单调递减;(3)
 时,
时, ,
, .--------2分
.--------2分 ,即
,即 ,即
,即 ,
, .
. 函数f(x)的单调递增区间是
函数f(x)的单调递增区间是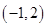 .-------4分
.-------4分 对
对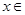 R都成立,-------6分
R都成立,-------6分 对
对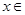 R都成立, 即
R都成立, 即 对
对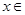 R都成立.
R都成立. ,解得
,解得 .
. 当
当 时, 函数f(x)在R上单调递减.---------9分
时, 函数f(x)在R上单调递减.---------9分 对
对 都成立,
都成立,
 对
对 都成立.
都成立. 对
对 都成立.---------11分
都成立.---------11分 ,则
,则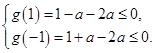 解得
解得
 .-----------14分
.-----------14分 函数f(x)在
函数f(x)在 上单调递增,
上单调递增, 对
对 都成立,
都成立, 
 对
对 都成立
都成立 对
对 都成立,即
都成立,即 对
对 都成立.----11分
都成立.----11分 , 则
, 则 .------12分
.------12分 时,
时, ;当
;当 时,
时, .
. 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增. ,
, 在
在 上的最大值是
上的最大值是 .
.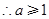 .-----------14分
.-----------14分

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:不详 题型:解答题
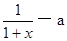 ,(f/(x))是f(x)的导数)
,(f/(x))是f(x)的导数)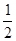
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
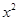 ,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;
,若函数F(x)=f(x)+g(x),求函数F(x)的单调区间;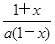 ,函数G(x)=h(x)·f(x),若对任意x∈(0,1),
,函数G(x)=h(x)·f(x),若对任意x∈(0,1),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com