练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校将一次测试中高三年级学生的数学成绩统计如下表所示，在参加测试的学生中任取1人，其成绩不低于120分的概率为.

    分数

    频数

    40

    50

    70

    60

    80

    50

    （1）求的值；

    （2）若按照分层抽样的方法从成绩在、的学生中抽取6人，再从这6人中随机抽取2人进行错题分析，求这2人中至少有1人的分数在的概率.

    【答案】（1）；（2）

    【解析】

    （1）根据频率的概念，可得结果.

    （2）根据分层抽样的方法，得到成绩在、分别抽出的人数，并对这些学生分别进行标记，然后利用列举法，结合古典概型的概念，可得结果.

    （1）依题意：，解得.

    （2）依题意：

    成绩在的学生抽取2人，记为，

    成绩在的学生抽取4人，记为，

    则任取2人，所有的情况为

    ，

    ，共15种，

    其中满足条件的为

    ，共9种，

    故所求概率.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】一款击鼓小游戏的规则如下：每盘游戏都需击鼓三次，每次击鼓后要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现三次音乐获得150分，出现两次音乐获得100分，出现一次音乐获得50分，没有出现音乐则获得-300分.设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立.

    （1）若一盘游戏中仅出现一次音乐的概率为，求的最大值点；

    （2）以（1）中确定的作为的值，玩3盘游戏，出现音乐的盘数为随机变量，求每盘游戏出现音乐的概率，及随机变量的期望；

    （3）玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】汽车是碳排放量比较大的行业之一，欧盟规定，从2015年开始，将对排放量超过130g/km的型新车进行惩罚（视为排放量超标），某检测单位对甲、乙两类型品牌抽取5辆进行排放量检测，记录如下（单位：g/km）：

    甲

    80

    110

    120

    140

    150

    乙

    100

    120

    x

    y

    160

    经测算发现，乙品牌车排放量的平均值为.

    （Ⅰ）从被检测的5辆甲类品牌中任取2辆，则至少有一辆排放量超标的概率是多少?

    （Ⅱ）若乙类品牌的车比甲类品牌的的排放量的稳定性要好，求x的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某次数学知识比赛中共有6个不同的题目，每位同学从中随机抽取3个题目进行作答，已知这6个题目中，甲只能正确作答其中的4个，而乙正确作答每个题目的概率均为，且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.

    （1）求甲、乙两位同学总共正确作答3个题目的概率；

    （2）若甲、乙两位同学答对题目个数分别是，，由于甲所在班级少一名学生参赛，故甲答对一题得15分，乙答对一题得10分，求甲乙两人得分之和的期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）证明：当时，；

    （2）若时不等式成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有橡皮泥制作的底面半径为5，高为9的圆锥和底面半径为，高为8的圆柱各一个.若将它们重新制作成总体积与各自的高均保持不变，但底面半径相同的新的圆锥与圆柱各一个，则新的底面半径为_________；若新圆锥的内接正三棱柱表面积取到最大值，则此正三棱柱的底面边长为_________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

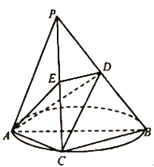
    【题目】如图，是一个三棱锥，是圆的直径，是圆上的点，垂直圆所在的平面，，分别是棱，的中点.

    （1）求证：平面；

    （2）若二面角是，，求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，点满足方程.

    （1）求点M的轨迹C的方程；

    （2）作曲线C关于轴对称的曲线，记为，在曲线C上任取一点，过点P作曲线C的切线l，若切线l与曲线交于A，B两点，过点A，B分别作曲线的切线，证明的交点必在曲线C上.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线（为参数），将曲线上的所有点的横坐标保持不变，纵坐标缩短为原来的后得到曲线；以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.

    （1）求曲线和直线的直角坐标方程；

    （2）已知，设直线与曲线交于不同的、两点，求的值.

    查看答案和解析>>

    同步练习册答案