
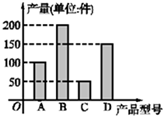
 (2012•房山区二模)某工厂2011年生产的A,B,C,D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加今年五月份的一个展销会.
(2012•房山区二模)某工厂2011年生产的A,B,C,D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加今年五月份的一个展销会.| 50 |
| 500 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
| C | 2 50 |
| C | 2 10 |
| C | 2 20 |
| C | 2 5 |
| C | 2 15 |
| 350 |
| 1225 |
| 5 |
| 7 |
| ||
|
| 10 |
| 455 |
| ||||
|
| 100 |
| 455 |
| ||||
|
| 225 |
| 455 |
| ||
|
| 120 |
| 455 |
| P | 0 | 1 | 2 | 3 | ||||||||
| X |
|
|
|
|
| 10 |
| 455 |
| 100 |
| 455 |
| 225 |
| 455 |
| 120 |
| 455 |


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:高中数学 来源: 题型:
| xf′(x)-f(x) |
| x2 |
| f(x) |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com