
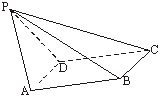
(Ⅰ)求点P到平面ABCD的距离;
(Ⅱ)求面APB与面CPB所成二面角的大小.
20.本小题主要考查棱锥、二面角和线面关系等基本知识,同时考查空间想象能力和推理、运算能力.
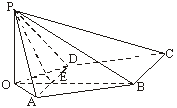
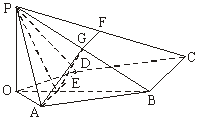
(Ⅰ)解:如图,作PO⊥平面ABCD,垂足为点O.
连结OB、OA、OD,OB与AD交于点E,连结PE.
∵AD⊥PB,∴AD⊥OB,
∵PA=PD,∴OA=OD,
于是OB平分AD,点E为AD的中点,所以PE⊥AD.由此知∠PEB为面PAD与面ABCD所成二面角的平面角,
∴∠PEB=120°,∠PEO=60°.
由已知可求得PE=![]() ,
,
∴PO=PE·sin60°=![]() ×
×![]() =
=![]() ,
,
即点P到平面ABCD的距离为![]() .
.
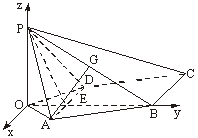
(Ⅱ)解法一:
如图建立直角坐标系,其中O为坐标原点,x轴平行于DA.
P(0,0,![]() ),B(0,
),B(0,![]() ,0),
,0),
PB中点G的坐标为(0,![]() ,
,![]() ),连结AG.
),连结AG.
又知A(1,![]() ,0),C(-2,
,0),C(-2,![]() ,0).
,0).
由此得到
![]() =(1,-
=(1,-![]() ,-
,-![]() ),
),![]() =(0,
=(0,![]() ,-
,-![]() ),
),
![]() =(-2,0,0).
=(-2,0,0).
于是有![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,
=0,
所以![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() .
.![]() ,
,![]() 的夹角θ等于所求二面角的平面角,
的夹角θ等于所求二面角的平面角,
于是cosθ=![]() =-
=-![]() ,
,
所以所求二面角的大小为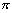 -arccos
-arccos![]() .
.
解法二:如图,取PB的中点G,PC的中点F,连结EG、AG、GF,则AG⊥PB,FG∥BC,FG=![]() BC.
BC.
∵AD⊥PB,∴BC⊥PB,FG⊥PB,
∴∠AGF是所求二面角的平面角.
∵AD⊥面POB,∴AD⊥EG.
又∵PE=BE,
∴EG⊥PB,且∠PEG=60°.
在Rt△PEG中,EG=PE·cos60°=![]() ,
,
在Rt△GAE中,AE=![]() AD=1,
AD=1,
于是tanGAE=![]() =
=![]() ,
,
又∠AGF=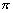 -∠GAE,
-∠GAE,
所以所求二面角的大小为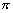 -arctan
-arctan![]() .
.


科目:高中数学 来源: 题型:
 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.8
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,| PN |
| 1 |
| 2 |
| NC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com