
 (a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1。
(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1。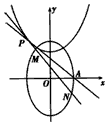
解:(1)由题意,得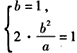 从而  因此,所求的椭圆方程为  ; ; |
|
(2)如图,设 则抛物线C2在点P处的切线斜率为  直线MN的方程为:y=2tx-t2+h 将上式代入椭圆C1的方程中,得4x2+(2tx-t2+h)2-4=0 即  ① ①因为直线MN与椭圆C1有两个不同的交点, 所以①式中的Δ=16[-t4+2(h+2)t2-h2+4] >0 ② 设线段MN的中点的横坐标是x3,则  设线段PA的中点的横坐标是x4,则 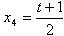 由题意,得x3=x4,即t2+(1+h)t+1=0 ③ 由③式中的Δ2=(1+h)2-4≥0,得h≥1或h≤-3 当h≤-3时,h+2<0,4-h2<0,则不等式②不成立, 所以h≥1 当h=1时,代入方程③得t=-1 将h=1,t=-1代入不等式②,检验成立, 所以,h的最小值为1。 |
 |


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源:2012-2013学年广东省肇庆四中高三(上)第二次月考数学试卷(文科)(解析版) 题型:解答题
 (a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省厦门二中高二(上)期末数学复习试卷7(文科)(解析版) 题型:解答题
 (a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.查看答案和解析>>
科目:高中数学 来源:2012-2013学年海南省乐东县民族中学高三(上)第三次月考数学试卷(文科)(解析版) 题型:解答题
 (a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省赣州三中、于都中学高三联考数学试卷(文科)(解析版) 题型:解答题
 (a>b>0)的右顶点A(1,0),过C1的焦点且垂直长轴的弦长为1.
(a>b>0)的右顶点A(1,0),过C1的焦点且垂直长轴的弦长为1.查看答案和解析>>
科目:高中数学 来源:2012年广东省湛江市高考数学二模试卷(文科)(解析版) 题型:解答题
 (a>b>0)的左、右顶点分别是A、B,P是双曲线C2:
(a>b>0)的左、右顶点分别是A、B,P是双曲线C2: =1右支x轴上方的一点,连接AP交椭圆于点C,连接PB并延长交椭圆于点D.
=1右支x轴上方的一点,连接AP交椭圆于点C,连接PB并延长交椭圆于点D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com