
已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.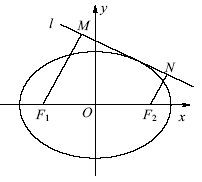
(1)求椭圆C的方程;
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l.求四边形F1MNF2面积S的最大值.
(1)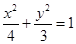 ;(2)
;(2)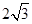 。
。
解析试题分析:(1)依题意,设椭圆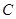 的方程为
的方程为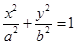 .
.
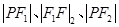 构成等差数列,
构成等差数列,
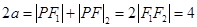 ,
, 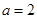 .
.
又 ,
,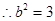 .
. 椭圆
椭圆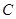 的方程为
的方程为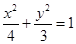 . 4分
. 4分
(2) 将直线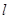 的方程
的方程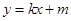 代入椭圆
代入椭圆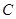 的方程
的方程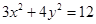 中,得
中,得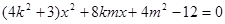 . 5分
. 5分
由直线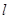 与椭圆
与椭圆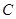 仅有一个公共点知,
仅有一个公共点知,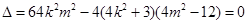 ,
,
化简得: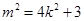 . 7分
. 7分
设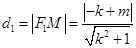 ,
,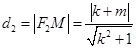 , 9分
, 9分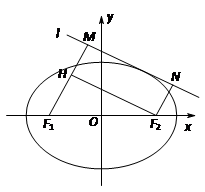
(法一)当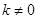 时,设直线
时,设直线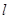 的倾斜角为
的倾斜角为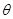 ,
,
则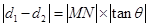 ,
,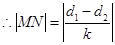 ,
, 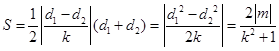
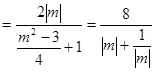 ,11分
,11分
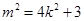 ,
, 当
当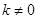 时,
时,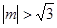 ,
,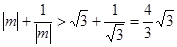 ,
,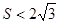 .
.
当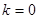 时,四边形
时,四边形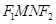 是矩形,
是矩形,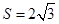 . 13分
. 13分
所以四边形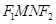 面积
面积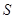 的最大值为
的最大值为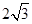 . 14分
. 14分
(法二)
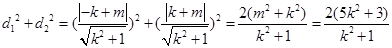 ,
, 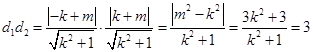 .
. 
 .
.
四边形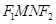 的面积
的面积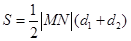
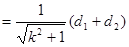 , 11分
, 11分 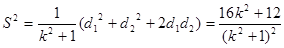
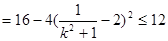 . 13分
. 13分
当且仅当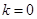 时,
时,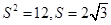 ,故
,故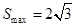 .
.
所以四边形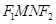 的面积
的面积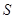 的最大值为
的最大值为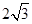 . 14分
. 14分
考点:椭圆的标准方程;椭圆的简单性质;椭圆的定义;直线与椭圆的综合应用;基本不等式。
点评:(1)本题主要考查椭圆的方程与性质、直线方程、直线与椭圆的位置关系等基础知
识,考查学生运算能力、推理论证以及分析问题、解决问题的能力,考查分类讨论、数形结合、化归与转化思想.(2)做此题的关键是表示出四边形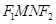 的面
的面


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
已知椭圆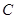 的中心为坐标原点
的中心为坐标原点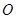 ,一个长轴端点为
,一个长轴端点为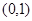 ,短轴端点和焦点所组成的四边形为正方形,若直线
,短轴端点和焦点所组成的四边形为正方形,若直线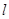 与
与 轴交于点
轴交于点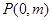 ,与椭圆
,与椭圆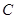 交于不同的两点
交于不同的两点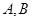 ,且
,且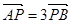 。(14分)
。(14分)
(1)求椭圆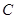 的方程;
的方程;
(2)求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆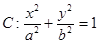 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点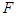 的最短距离为
的最短距离为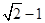 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点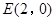 且斜率为
且斜率为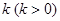 的直线
的直线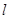 与
与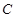 交于
交于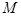 、
、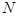 两点,
两点,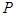 是点
是点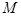 关于
关于 轴的对称点,证明:
轴的对称点,证明: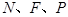 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图所示,将一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上,  点在
点在 上,且对角线
上,且对角线 过点
过点 ,已知
,已知 米,
米,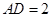 米.
米.
(1)要使矩形 的面积大于32平方米,则
的面积大于32平方米,则 的长应在什么范围内?
的长应在什么范围内?
(2)当 的长度为多少时,矩形花坛
的长度为多少时,矩形花坛 的面积最小?并求出最小值.
的面积最小?并求出最小值.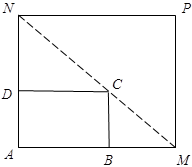
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
设椭圆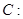
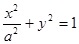 (
(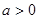 )的两个焦点是
)的两个焦点是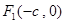 和
和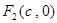 (
(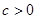 ),且椭圆
),且椭圆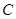 与圆
与圆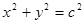 有公共点.
有公共点.
(1)求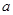 的取值范围;
的取值范围;
(2)若椭圆上的点到焦点的最短距离为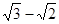 ,求椭圆的方程;
,求椭圆的方程;
(3)对(2)中的椭圆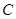 ,直线
,直线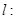
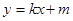 (
(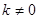 )与
)与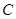 交于不同的两点
交于不同的两点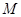 、
、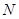 ,若线段
,若线段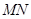 的垂直平分线恒过点
的垂直平分线恒过点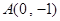 ,求实数
,求实数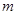 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,已知点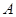 是椭圆
是椭圆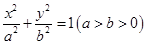 的右顶点,若点
的右顶点,若点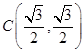 在椭圆上,且满足
在椭圆上,且满足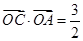 .(其中
.(其中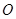 为坐标原点)
为坐标原点)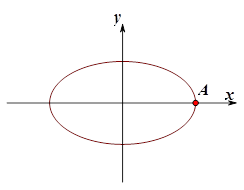
(1)求椭圆的方程;
(2)若直线 与椭圆交于两点
与椭圆交于两点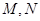 ,当
,当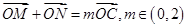 时,求
时,求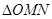 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知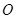 为坐标原点,点
为坐标原点,点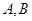 分别在
分别在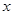 轴
轴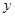 轴上运动,且
轴上运动,且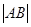 =8,动点
=8,动点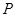 满足
满足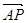 =
=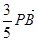 ,设点
,设点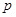 的轨迹为曲线
的轨迹为曲线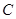 ,定点为
,定点为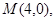 直线
直线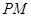 交曲线
交曲线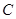 于另外一点
于另外一点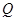
(1)求曲线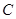 的方程;
的方程;
(2)求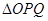 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在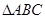 中,两个定点
中,两个定点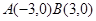 ,
,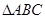 的垂心H(三角形三条高线的交点)是AB边上高线CD的中点。
的垂心H(三角形三条高线的交点)是AB边上高线CD的中点。
(1)求动点C的轨迹方程;
(2)斜率为2的直线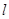 交动点C的轨迹于P、Q两点,求
交动点C的轨迹于P、Q两点,求 面积的最大值(O是坐标原点)。
面积的最大值(O是坐标原点)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com