

(Ⅰ)求证AB⊥BC;
(Ⅱ)如果AB=BC=2![]() ,求侧面PBC与侧面PAC所成二面角的大小.
,求侧面PBC与侧面PAC所成二面角的大小.
21. 本小题主要考查两个平面垂直的性质、二面角等有关知识,以及逻辑思维能力和空间想象能力.
(Ⅰ)证明:如图,取AC中点D,连结PD、BD.

因为PA=PC,所以PD⊥AC,
又已知面PAC⊥面ABC,
所以PD⊥面ABC,D为垂足.
因为PA=PB=PC,
所以DA=DB=DC,可知AC为△ABC的外接圆直径,
因此AB⊥BC.
(Ⅱ)解:因为AB=BC,D为AC中点,
所以BD⊥AC.
又面PAC⊥面ABC,
所以BD⊥平面PAC,D为垂足.
作BE⊥PC于E,连结DE,
因为DE为BE在平面PAC内的射影,
所以DE⊥PC,∠BED为所求二面角的平面角.
在Rt△ABC中,AB=BC=2![]() ,所以BD=
,所以BD=![]() .
.
在Rt△PDC中,PC=3,DC=![]() ,PD=
,PD=![]() ,
,
所以DE=![]() =
=![]() =
=![]() .
.
因此,在Rt△BDE中,tanBED=![]() =
=![]() ,∠BED=60°,
,∠BED=60°,
所以侧面PBC与侧面PAC所成的二面角为60°.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:
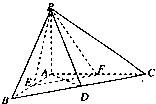 如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=
如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
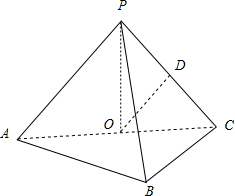 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
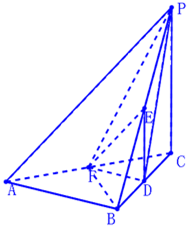 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com