
【题目】已知函数g(x)=ax2﹣2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|),x∈R;
(1)求实数a、b的值;
(2)若不等式 ![]() 对任意x∈R恒成立,求实数k的范围;
对任意x∈R恒成立,求实数k的范围;
(3)对于定义在[p,q]上的函数m(x),设x0=p,xn=q,用任意xi(i=1,2,…,n﹣1)将[p,q]划分成n个小区间,其中xi﹣1<xi<xi+1 , 若存在一个常数M>0,使得不等式|m(x0)﹣m(x1)|+|m(x1)﹣m(x2)|+…+|m(xn﹣1)﹣m(xn)|≤M恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试证明函数f(x)是在[1,3]上的有界变差函数,并求出M的最小值.
【答案】
(1)解:∵函数g(x)=ax2﹣2ax+1+b,
∵a>0,对称轴x=1,
∴g(x)在区间[2,3]上是增函数,
又∵函数g(x)故在区间[2,3]上的最大值为4,最小值为1,
∴ 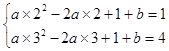 ,
,
解得:a=1,b=0.
∴g(x)=x2﹣2x+1
故实数a的值为1,b的值为0.
(2)解:由(1)可知g(x)=x2﹣2x+1,
∵f(x)=g(|x|),
∴f(x)=x2﹣2|x|+1,
∵ ![]() 对任意x∈R恒成立,
对任意x∈R恒成立,
令F(x)=f(x)+g(x)=x2﹣2x+1+x2﹣2|x|+1= 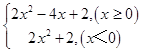
根据二次函数的图象及性质可得F(x)min=f(1)=0
则F(x)min≥ ![]() 恒成立,即:
恒成立,即: ![]() ≤0
≤0
令log2k=t,
则有:t2﹣2t﹣3≤0,
解得:﹣1≤t≤3,
即 ![]() ,
,
得: ![]()
故得实数k的范围为 ![]()
(3)解:函数f(x)为[1,3]上的有界变差函数.
因为函数f(x)为[1,3]上的单调递增函数,且对任意划分T:1=x0<x1<…<xi<…<xn=3
有f(1)=f(x0)<f(x1)<…<f(xI)<…<f(xn)=f(3)
所以 ![]() |m(xi)﹣m(xi﹣1)|=f(x1)﹣f(x0)+f(x2)﹣f(x1)<…<f(xn)﹣f(xn﹣1)
|m(xi)﹣m(xi﹣1)|=f(x1)﹣f(x0)+f(x2)﹣f(x1)<…<f(xn)﹣f(xn﹣1)
=f(xn)﹣f(x0)=f(3)﹣f(1)=4恒成立,
所以存在常数M,使得 ![]() |m(xi)﹣m(xi﹣1)|≤M是恒成立.
|m(xi)﹣m(xi﹣1)|≤M是恒成立.
M的最小值为4,即Mmin=4
【解析】(1)由已知中g(x)在区间[2,3]的最大值为4,最小值为1,结合函数的单调性及最值,我们易构造出关于a,b的方程组,解得a,b的值;(2)求出f(x), ![]() 对任意x∈R恒成立等价于F(x)min=f(x)+g(x)恒成立,求实数k的范围;根据有界变差函数的定义,我们先将区间[1,3]进行划分,进而判断
对任意x∈R恒成立等价于F(x)min=f(x)+g(x)恒成立,求实数k的范围;根据有界变差函数的定义,我们先将区间[1,3]进行划分,进而判断 ![]() |m(xi)﹣m(xi﹣1)|≤M是否恒成立,进而得到结论.
|m(xi)﹣m(xi﹣1)|≤M是否恒成立,进而得到结论.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=|2x﹣1|+|5x﹣1|
(1)求f(x)>x+1的解集;
(2)若m=2﹣n,对m,n∈(0,+∞),恒有 ![]() 成立,求实数x的范围.
成立,求实数x的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1 , 抛物线C2焦点均在x轴上,C1的中心和C2顶点均为原点O,从每条曲线上各取两个点,将其坐标记录于表中,则C1的左焦点到C2的准线之间的距离为( )
x | 3 | ﹣2 | 4 |
|
y | -2 | 0 | ﹣4 |
|
A.![]() -1
-1
B.![]() -1
-1
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是集合{x|x=3s+3t , s<t且s,t∈N}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图的等腰直角三角形数表,则a15的值为 . 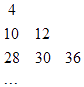
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处. 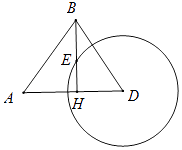
(1)求此时该外国船只与D岛的距离;
(2)观测中发现,此外国船只正以每小时4海里的速度沿正南方航行.为了将该船拦截在离D岛12海里的E处(E在B的正南方向),不让其进入D岛12海里内的海域,试确定海监船的航向,并求其速度的最小值(角度精确到0.1°,速度精确到0.1海里/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,AB=1,BB1=2,求: 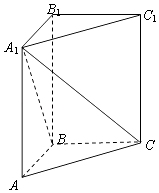
(1)异面直线B1C1与A1C所成角的大小;
(2)四棱锥A1﹣B1BCC1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,3,则输出v的值为( ) 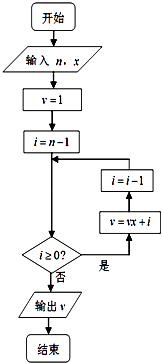
A.20
B.61
C.183
D.548
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com