Question

【题目】设函数f（x）=a﹣ ，
（1）若x∈[ ，+∞），①判断函数g（x）=f（x）﹣2x的单调性并加以证明；②如果f（x）≤2x恒成立，求a的取值范围；
（2）若总存在m，n使得当x∈[m，n]时，恰有f（x）∈[2m，2n]，求a的取值范围．

Answer 1

【答案】
（1）解：①x∈[ ，+∞）时，g（x）=f（x）﹣2x=a﹣ ．

任取 ，

= ．

∵ ，∴x2﹣x10，x1x2＞0．

∴g（x1）﹣g（x2）＜0，g（x1）＜g（x2）．

∴g（x）在[ ，+∞）上单调递减．

②f（x）≤2xg（x）≤0，∵g（x）在[ ，+∞）上单调递减，

∴ ，∴

（2）解：∵f（x）=a﹣ 的定义域为（﹣∞，0）∪（0，+∞），∴mn＞0

若n＞m＞0，则 ，且在[m，n]上递增，∴ ，∴ ．

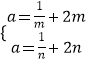∴m，n是 的两个根，即2x2﹣ax+1=0的两个根，

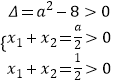∴ ，解得 ．

若m＜n＜0，则f（x）=a+ ，且在[m，n]上递减，

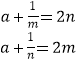∴ ，∴ ，相减得：mn= ，代回得：a=0．

综上所得：a的取值范围是（ ）∪{0}

【解析】（1）①把f（x）的解析式代入后，直接利用函数的单调性的定义证明；②由①中的单调性求出g（x）的最大值，由最大值小于等于0求解a的范围；（2）求出函数的定义域，然后分m，n同正和同负两种情况分析，借助于函数的单调性的方程组，然后再转化为方程的根进行分析．
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较．