甲、乙两队进行球类比赛,约定先胜3局获胜,比赛结束.假设在每局比赛中,甲队获胜的概率为0.6,乙队获胜的概率为0.4,各局比赛相互独立.已知第一局比赛已经结束,且甲队获胜.
(1)求甲队获得这次比赛胜利的概率;
(2)设ξ表示从第二局开始到比赛结束所进行的局数,求ξ的分布列和数学期望.
【答案】
分析:(1)甲队获胜有三种情形,①3:0,②3:1,③3:2,其每种情形的最后一局肯定是甲队胜,分别求出相应的概率,最后根据互斥事件的概率公式求出甲队获得这次比赛胜利的概率;
(2)ξ的取值可能为2,3,4,然后利用相互独立事件的概率乘法公式求出相应的概率,列出分布列,最后根据数学期望公式解之即可.
解答:解:(1)甲队获胜有三种情形,其每种情形的最后一局肯定是甲队胜
①3:0,概率为P
1=0.6
2=0.36
②3:1,概率为P
2=
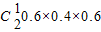
=0.288
③3:2,概率为P
3=
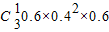
=0.1728
∴甲队获得这次比赛胜利的概率为P=P
1+P
2+P
3=0.36+0.288+0.1728=0.8208;
(2)ξ的取值可能为2,3,4
P(ξ=2)=0.6
2=0.36
P(ξ=3)=
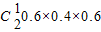
+0.4
3=0.352
P(ξ=4)=
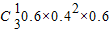
+

=0.288
则ξ的分布列为
| ξ | 2 | 3 | 4 |
| P | 0.36 | 0.352 | 0.288 |
∴E(ξ)=2×0.36+3×0.352+4×0.288=2.928
点评:本题主要考查了相互独立事件的概率乘法公式,以及离散型随机变量的期望与分布列,同时考查了分类讨论的数学思想,属于中档题.

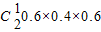 =0.288
=0.288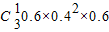 =0.1728
=0.1728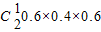 +0.43=0.352
+0.43=0.352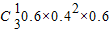 +
+ =0.288
=0.288
