Question

设p：实数x满足x²－4ax＋3a²＜0（其中a≠0），q：实数x满足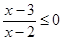

(1)若a＝1，且p∧q为真，求实数x的取值范围；

(2)若p是q的必要不充分条件，求实数a的取值范围．

 

Answer 1

【答案】

(1) (2,3) (2) (1,2]

【解析】

试题分析：(1)当a＝1时，解得1＜x＜3，即p为真时实数x的取值范围是1＜x＜3. 2分

由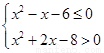，得2＜x≤3，即q为真时实数x的取值范围是2＜x≤3. 4分

若p∧q为真，则p真且q真，5分

所以实数x的取值范围是(2,3)．7分

(2)p是q的必要不充分条件，即q?p，且p/?q，8分

设A＝{x|p(x)}，B＝{x|q(x)}，则A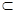B，又B＝(2,3]，

由x²－4ax＋3a²＜0得(x－3a)(x－a)＜0，9分

当a＞0时，A＝(a,3a)，有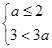，解得1＜a≤2；11分

当a＜0时，A＝(3a，a)，显然A∩B＝?，不合题意．13分

所以实数a的取值范围是(1,2]．15分

考点：解不等式及复合命题，集合包含关系

点评：复合命题p∧q的真假由命题p，q共同决定，当两命题中有一个是真命题时复合后为真命题，

由若p是q的必要不充分条件可得集合p是集合q的真子集