Question

已知a，b为正常数，（ax-1）³（x+b）⁴的展开式中的常数项为-1，x的一次项系数为2，则a=    ，b=    ．

Answer 1

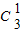
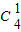
【答案】分析：依题意，（-1）³•b⁴=-1，•（ax）•（-1）²•b⁴+（-1）³•x¹•b³=2x，a，b为正常数，可先求得b的值，再求a的值．
解答：解：依题意，（ax-1）³（x+b）⁴的展开式中的常数项为-1，
∴（-1）³•b⁴=-1，
∴b⁴=1，又b＞0，
∴b=1；
又（ax-1）³（x+b）⁴的展开式中x的一次项系数为2，
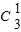
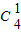
∴•（ax）•（-1）²•b⁴+（-1）³•x¹•b³=2x，即3a-4=2，
∴a=2，
综上所述，a=2，b=1．
故答案为：2，1．
点评：本题考查二项式定理，着重考查二项展开式的通项公式的灵活应用，考查运算能力，属于中档题．