
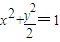 上的点,O为原点,OA与OB斜率的乘积等于-2,
上的点,O为原点,OA与OB斜率的乘积等于-2,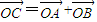 .
.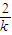 ,点A坐标方程组
,点A坐标方程组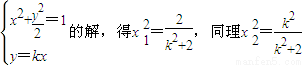 ,|x1+x2|=
,|x1+x2|=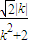 .|OA|=
.|OA|=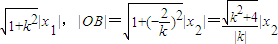 |,tan∠AOB=|
|,tan∠AOB=|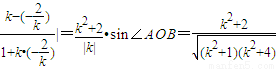 ,再由S=2S△AOB=|OA||OB|sin∠AOB
,再由S=2S△AOB=|OA||OB|sin∠AOB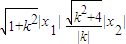
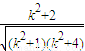 ,能求出四边形OACB的面积.
,能求出四边形OACB的面积.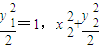 =1,
=1,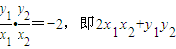 =0,…(2分)
=0,…(2分)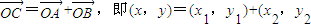 ),
),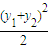
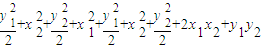 =2,
=2, =1上. …(5分)
=1上. …(5分) ,
,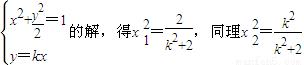 ,∴|x1+x2|=
,∴|x1+x2|=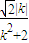 .…(8分)
.…(8分)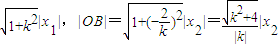 |,
|, ,
,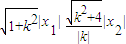
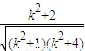
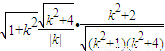
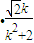
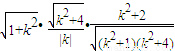
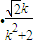
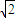 .
.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 3 |
| AF2 |
| F2B |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
| a |
| a2-b2 |
| a |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年北京市西城区高二(上)期末数学试卷(文科)(解析版) 题型:解答题
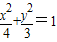 .
.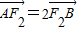 ,求直线AB的斜率.
,求直线AB的斜率.查看答案和解析>>
科目:高中数学 来源:2010年河北省唐山市高考数学二模试卷(理科)(解析版) 题型:解答题
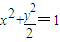 上的点,O为原点,OA与OB斜率的乘积等于-2,
上的点,O为原点,OA与OB斜率的乘积等于-2,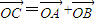 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com