
【题目】在四棱锥P–ABCD中,![]() ,
,![]() .
.
(1)设AC与BD相交于点M,![]() ,且
,且![]() 平面PCD,求实数m的值;
平面PCD,求实数m的值;
(2)若![]() ,
,![]() ,
,![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

【答案】(1)![]()
(2)![]()
【解析】
(1)由AB∥CD,得到![]() ,由MN∥平面PCD,得MN∥PC,从而
,由MN∥平面PCD,得MN∥PC,从而![]() ,由此能实数m的值;
,由此能实数m的值;
(2)由AB=AD,∠BAD=60°,知△ABD为等边三角形,推导出PD⊥DB,PD⊥AD,从而PD⊥平面ABCD,以D为坐标原点,![]() 的方向为x,y轴的正方向建立空间直角坐标系,由此能求出二面角B﹣PC﹣B的余弦值.
的方向为x,y轴的正方向建立空间直角坐标系,由此能求出二面角B﹣PC﹣B的余弦值.
解:(1)因为![]() ,所以
,所以![]() ,即
,即![]() .
.
因为![]() 平面PCD,
平面PCD,![]() 平面PAC,平面
平面PAC,平面![]() 平面
平面![]() ,
,
所以![]() .
.
所以![]() ,即
,即![]() .
.
(2)因为![]() ,
,![]() ,可知
,可知![]() 为等边三角形,
为等边三角形,
所以![]() ,又
,又![]() ,
,
故![]() ,所以
,所以![]() .
.
由已知![]() ,
,![]() ,所以
,所以![]() 平面ABCD,
平面ABCD,
如图,以D为坐标原点,![]() 的方向为x,y轴的正方向建立空间直角坐标系,
的方向为x,y轴的正方向建立空间直角坐标系,
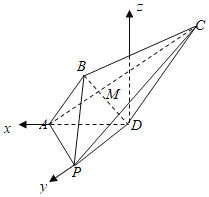
设![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,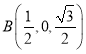 ,
,![]() ,
,![]() ,
,
则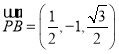 ,
,![]() ,
,![]()
设平面PBC的一个法向量为![]() ,则有
,则有
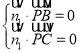 即
即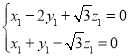 .
.
令![]() ,则
,则![]() ,即
,即![]() ,
,
设平面APC的一个法向量为![]() ,则有
,则有
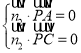 ,即
,即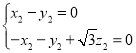
令![]() ,则
,则![]() ,即
,即![]() .
.
所以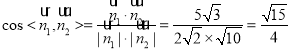
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数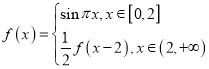 ,有下列说法:
,有下列说法:
①函数![]() 对任意
对任意![]() ,都有
,都有![]() 成立;
成立;
②函数![]() 在
在![]() 上单调递减;
上单调递减;
③函数![]() 在
在![]() 上有3个零点;
上有3个零点;
④若函数![]() 的值域为
的值域为![]() ,设
,设![]() 是
是![]() 中所有有理数的集合,若简分数
中所有有理数的集合,若简分数![]() (其中
(其中![]() ,
,![]() 为互质的整数),定义函数
为互质的整数),定义函数![]() ,则
,则![]() 在
在![]() 中根的个数为5;
中根的个数为5;
其中正确的序号是______(填写所有正确结论的番号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(m+2)![]() 是幂函数,设a=log54,b=
是幂函数,设a=log54,b=![]() ,c=0.5–0.2,则f(a),f(b),f(c)的大小关系是
,c=0.5–0.2,则f(a),f(b),f(c)的大小关系是
A.f(a)<f(b)<f(c)B.f(b)<f(c)<f(a)
C.f(c)<f(b)<f(a)D.f(c)<f(a)<f(b)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C:![]() 的左、右焦点为F1,F2,直线y
的左、右焦点为F1,F2,直线y![]() b与C的右支相交于点P,若|PF1|=2|PF2|,则双曲线C的离心率为_____;若该双曲线的焦点到其渐近线的距离是
b与C的右支相交于点P,若|PF1|=2|PF2|,则双曲线C的离心率为_____;若该双曲线的焦点到其渐近线的距离是![]() ,则双曲线的方程为_____.
,则双曲线的方程为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四川省阆中中学某部根据运动场地的影响,但为尽大可能让学生都参与到运动会中来,在2018春季运动会中设置了五个项目,其中属于跑步类的两项,分别是200米和400米,另外三项分别为跳绳、跳远、跳高![]() 学校要求每位学生必须参加,且只参加其中一项,学校780名同学参加各运动项目人数统计如下条形图:
学校要求每位学生必须参加,且只参加其中一项,学校780名同学参加各运动项目人数统计如下条形图:

其中参加跑步类的人数所占频率为![]() ,为了了解学生身体健康与参加运动项目之间的关系,用分层抽样的方法从这780名学生中抽取13人进行分析.
,为了了解学生身体健康与参加运动项目之间的关系,用分层抽样的方法从这780名学生中抽取13人进行分析.
![]() 1
1![]() 求条形图中m和n的值以及抽取的13人中参加200米的学生人数;
求条形图中m和n的值以及抽取的13人中参加200米的学生人数;
![]() 2
2![]() 现从抽取的参加400米和跳绳两个项目中随机抽取4人,记其中参加400米跑的学生人数为X,求离散型随机变量X的分布列与数学期望.
现从抽取的参加400米和跳绳两个项目中随机抽取4人,记其中参加400米跑的学生人数为X,求离散型随机变量X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com