
【题目】已知函数![]() ,
,![]() .
.
(1)设![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 处取得极大值,求实数
处取得极大值,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调增区间是![]() ,单调减函数是
,单调减函数是![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)![]() ,再次求导得
,再次求导得![]() ,由于
,由于![]() ,所以调增区间是
,所以调增区间是![]() ,单调减函数是
,单调减函数是![]() ;(2)
;(2)![]() 在
在![]() 处取得极大值,所以
处取得极大值,所以![]() .下面分成
.下面分成![]() ,
,![]() ,
,![]() 三类,讨论
三类,讨论![]() 单调区间,由此得出
单调区间,由此得出![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
当![]() 时,在
时,在![]() 上
上![]() ,
,![]() 单调递增;
单调递增;
在![]() 上
上![]() ,
,![]() 单调递减.
单调递减.
∴![]() 的单调增区间是
的单调增区间是![]() ,单调减函数是
,单调减函数是![]() .
.
(2)∵![]() 在
在![]() 处取得极大值,∴
处取得极大值,∴![]() .
.
①当![]() ,即
,即![]() 时,由(1)知,
时,由(1)知,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() ,
,![]() 单调递减,不合题意;
单调递减,不合题意;
②当![]() ,即
,即![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 处取得极小值,不合题意;
处取得极小值,不合题意;
③当![]() ,即
,即![]() 时,由(1)知,
时,由(1)知,![]() 在
在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() 取得极大值,满足条件.
取得极大值,满足条件.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
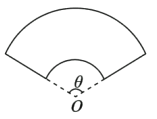
【题目】宜昌一中江南新校区拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米,设小圆弧所在圆的半径为![]() 米,圆心角
米,圆心角![]() (弧度).
(弧度).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米,设花坛的面积与装饰总费用之比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再向上平移1个单位长度,得到函数
个单位长度,再向上平移1个单位长度,得到函数![]() 的图象,则函数
的图象,则函数![]() 具有性质__________.(填入所有正确性质的序号)
具有性质__________.(填入所有正确性质的序号)
①最大值为![]() ,图象关于直线
,图象关于直线![]() 对称;
对称;
②图象关于![]() 轴对称;
轴对称;
③最小正周期为![]() ;
;
④图象关于点![]() 对称;
对称;
⑤在![]() 上单调递减
上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数据![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为
是杭州市100个普通职工的2016年10月份的收入(均不超过2万元),设这100个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上马云2016年10月份的收入
,如果再加上马云2016年10月份的收入![]() (约100亿元),则相对于
(约100亿元),则相对于![]() 、
、![]() 、
、![]() ,这101个月收入数据( )
,这101个月收入数据( )
A.平均数可能不变,中位数可能不变,方差可能不变
B.平均数大大增大,中位数可能不变,方差也不变
C.平均数大大增大,中位数一定变大,方差可能不变
D.平均数大大增大,中位数可能不变,方差变大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形![]() 的边长为1,如图所示:
的边长为1,如图所示:
(1)在正方形内任取一点![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)用芝麻颗粒将正方形均匀铺满,经清点,发现芝麻一共56粒,有44粒落在扇形![]() 内,请据此估计圆周率
内,请据此估计圆周率![]() 的近似值(精确到0.001).
的近似值(精确到0.001).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,若存在闭区间[m,n]
,若存在闭区间[m,n] ![]() D,使得函数
D,使得函数![]() 满足:①
满足:①![]() 在[m,n]上是单调函数;②
在[m,n]上是单调函数;②![]() 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com