
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点D在线段AB上,且满足
,点D在线段AB上,且满足![]() .
.

(1)求证:![]()
(2)当平面![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)首先取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,易证
,易证![]() 平面
平面![]() ,再利用线面垂直的性质即可证明
,再利用线面垂直的性质即可证明![]() .
.
(2)过点![]() 作
作![]() 于O,连
于O,连![]() ,
,![]() ,易证
,易证![]() ,得到
,得到![]() ,从而得到
,从而得到![]() 为二面角
为二面角![]() 的平面角,且
的平面角,且![]() .设
.设![]() ,利用余弦定理得到
,利用余弦定理得到![]() ,根据
,根据![]() 得到
得到
![]() ,利用三棱锥等体积转换得到
,利用三棱锥等体积转换得到![]() 到面
到面![]() 的距离为
的距离为![]() 的值,再求直线
的值,再求直线![]() 与平面
与平面![]() 所成角即可.
所成角即可.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
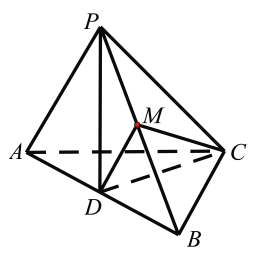
因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
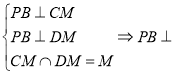 平面
平面![]() .
.
![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)过点![]() 作
作![]() 于O,连
于O,连![]() ,
,![]()

因为![]() ,
,![]() ,
,![]() 为公共边,
为公共边,
所以![]() ,即
,即![]() .
.
所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,
因为平面![]() 平面
平面![]() ,所以
,所以![]() .
.
令![]() ,则
,则![]() ,
,![]() ,
,
![]() .
.
平面![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() .
.
在![]() 中,由
中,由![]() ,
,
得![]() ,
,![]() ,所以
,所以![]() ,得
,得![]() .
.
又因为![]() ,记
,记![]() 到面
到面![]() 的距离为
的距离为![]() ,
,
![]() ,
,![]() .
.
![]() .
.
则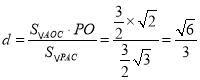 ,
,
记直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有下列四个结论:
,有下列四个结论:
①![]() 为偶函数;②
为偶函数;②![]() 的值域为
的值域为![]() ;
;
③![]() 在
在![]() 上单调递减;④
上单调递减;④![]() 在
在![]() 上恰有8个零点,
上恰有8个零点,
其中所有正确结论的序号为( )
A.①③B.②④C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,...,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表(如表)第1行的第4列和第5列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
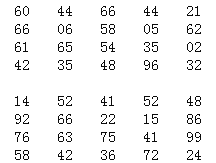
A.23B.21C.35D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求线段
上的动点,求线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离的最大值.并求此时点
的距离的最大值.并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为![]() ,写出
,写出![]() 的一个阿波罗尼斯圆的标准方程__________;②△
的一个阿波罗尼斯圆的标准方程__________;②△![]() 中,
中,![]() ,则当△
,则当△![]() 面积的最大值为
面积的最大值为![]() 时,
时,![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2是椭圆C:![]() (a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为
(a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过F1的直线l交椭圆于A,B两点,当△ABF2面积最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为![]() ,写出
,写出![]() 的一个阿波罗尼斯圆的标准方程__________;②△
的一个阿波罗尼斯圆的标准方程__________;②△![]() 中,
中,![]() ,则当△
,则当△![]() 面积的最大值为
面积的最大值为![]() 时,
时,![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
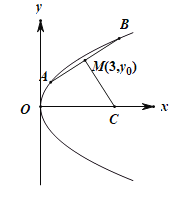
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com