
如图,在平面直角坐标系 中,以
中,以 轴为始边,两个锐角
轴为始边,两个锐角 ,
, 的终边分别与单位圆相交于A,B 两点.
的终边分别与单位圆相交于A,B 两点.
(Ⅰ)若 ,
, ,求
,求 的值;
的值;
(Ⅱ)若角 的终边与单位圆交于
的终边与单位圆交于 点,设角
点,设角 的正弦线分别为
的正弦线分别为 ,试问:以
,试问:以 作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由.
作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由.
(Ⅰ)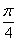 (Ⅱ)以
(Ⅱ)以 作为三边的长能构成一个三角形.
作为三边的长能构成一个三角形.
解析试题分析:(Ⅰ)∵0<α< , tanα=
, tanα=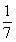 ,∴cosα=
,∴cosα= ,sinα=
,sinα= .
.
又∵0<β< ,sinβ=
,sinβ=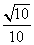 ,∴0<2β<π,cos2β=1-2sin2β=
,∴0<2β<π,cos2β=1-2sin2β=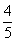 ,sin2β=
,sin2β=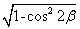 =
=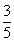 .
.
于是cos(α+2β)=cosαcos2β-sinαsin2β= ×
×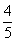 -
- ×
×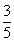 =
=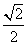 .
.
由已知条件知0<α+2β<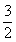 π,∴α+2β=
π,∴α+2β= . 6分
. 6分
(Ⅱ)解:以 作为三边的长能构成一个三角形,证明如下:
作为三边的长能构成一个三角形,证明如下:
∵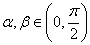 ,∴
,∴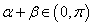
∴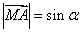 ,
,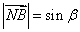 ,
,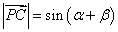
∵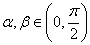 ,所以
,所以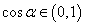 ,
,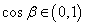 ,于是有:
,于是有: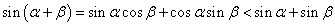 ① 8分
① 8分
又∵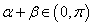 ,∴
,∴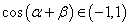 ,于是有:
,于是有: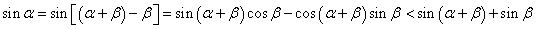 ②
②
同理: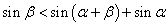 ③
③
由①②③可知,以 作为三边的长能构成一个三角形. 12分
作为三边的长能构成一个三角形. 12分
考点:同角间的三角函数关系及两角和的余弦公式
点评:第一问涉及到基本公式有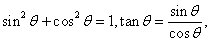
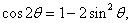
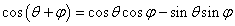 ,求角的大小常首先求角的某一三角函数值,结合角的范围即可求出;第二问判定能否构成三角形即判定三边长是否有任意两边之和大于第三边,确定不等式关系主要借助于正余弦函数的有解性
,求角的大小常首先求角的某一三角函数值,结合角的范围即可求出;第二问判定能否构成三角形即判定三边长是否有任意两边之和大于第三边,确定不等式关系主要借助于正余弦函数的有解性


科目:高中数学 来源: 题型:解答题
阅读下面材料:
根据两角和与差的正弦公式,有 ------①
------① ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明: ;
;
(Ⅱ)若 的三个内角
的三个内角 满足
满足 ,试判断
,试判断 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com